 por Jhonata » Dom Jul 21, 2013 12:32
por Jhonata » Dom Jul 21, 2013 12:32
Pessoal, surgiu mais uma dúvida, alguém aí pode me ajudar?
Seja S={

} e
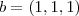
.
Determine a soma das coordenadas do vetor de S mais próximo de b.
Gabarito:

Desde já, obrigado!
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por e8group » Dom Jul 21, 2013 14:08
por e8group » Dom Jul 21, 2013 14:08
Boa tarde .Não verifiquei a resposta ,mas apresentarei um raciocínio para o exercício .O subconjunto

do

,mais precisamente ,

um é subespaço do

,seus vetores são os pontos

que satisfaz a propriedade do conjunto

que é
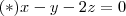
. Indo diretamente a geometria analítica ,seja
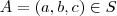
o ponto mais próximo de

.Definindo

vetor normal ao plano que passa pela origem de equação

e escolhendo um ponto arbitrário

em

(Escolha o ponto que você quiser,fique à vontade !) .
Próxima etapa :
Antes de tudo recomendo que faça um esboço da situação . Observando o triângulo retângulo , de catetos
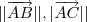
e hipotenusa

,fica fácil ver as seguintes relações :
(a)
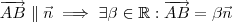
(b)

(c)

.
Partindo de (c) e usando (a) temos :
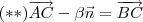
.Multiplicando-se escalarmente

por

e usando (b) , segue :

.
Logo ,

.
Assim , voltando em (a) temos :

. Agora já conseguimos obter o ponto

,pois já temos o ponto

,o ponto

e o vetor

.Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhonata » Dom Jul 21, 2013 14:16
por Jhonata » Dom Jul 21, 2013 14:16
santhiago escreveu:Boa tarde .Não verifiquei a resposta ,mas apresentarei um raciocínio para o exercício .O subconjunto

do

,mais precisamente ,

um é subespaço do

,seus vetores são os pontos

que satisfaz a propriedade do conjunto

que é
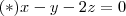
. Indo diretamente a geometria analítica ,seja
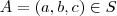
o ponto mais próximo de

.Definindo

vetor normal ao plano que passa pela origem de equação

e escolhendo um ponto arbitrário

em

(Escolha o ponto que você quiser,fique à vontade !) .
Próxima etapa :
Antes de tudo recomendo que faça um esboço da situação . Observando o triângulo retângulo , de catetos
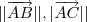
e hipotenusa

,fica fácil ver as seguintes relações :
(a)
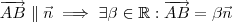
(b)

(c)

.
Partindo de (c) e usando (a) temos :
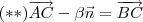
.Multiplicando-se escalarmente

por

e usando (b) , segue :

.
Logo ,

.
Assim , voltando em (a) temos :

. Agora já conseguimos obter o ponto

,pois já temos o ponto

,o ponto

e o vetor

.Tente concluir .
Muito bom. Tentarei aplicar o seu raciocínio nesta questão. Mas tendo em vista ser uma questão objetiva e de prova, acredito que haja algo mais simplório para a mesma.
De qualquer modo, muito obrigado Santhiago!
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por e8group » Dom Jul 21, 2013 14:29
por e8group » Dom Jul 21, 2013 14:29
santhiago escreveu:Muito bom. Tentarei aplicar o seu raciocínio nesta questão. Mas tendo em vista ser uma questão objetiva e de prova, acredito que haja algo mais simplório para a mesma.
De qualquer modo, muito obrigado Santhiago!
Não há de quê .Acho que uma forma mais simples(não sei é exatamente isto ) é aplicar a fórmula que fornece a distância de um ponto a um plano .Não lembro desta fórmula ,infelizmente tenho extrema dificuldade em decorar fórmulas .Sempre tenho que tirar um tempo a mais para deduzi-las ,a menos que tal dedução seja" trabalhosa" levando muito tempo para obtê-la .Neste caso,acho importante aplicar diretamente a fórmula ,mesmo assim é difícil lembrar .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Dom Jul 21, 2013 14:43
por e8group » Dom Jul 21, 2013 14:43
Se não cometi nenhum equívoco com o raciocínio o módulo do vetor
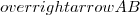
fornece a distância do ponto (1,1,1) ao plano de equação vide propriedade do conjunto S .Como só estamos queremos a soma das coordenadas do ponto A .Vamos verificar :

.
Escolhendo por exemplo

temos :
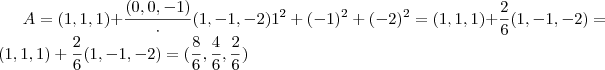
Logo ,

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jhonata » Dom Jul 21, 2013 14:54
por Jhonata » Dom Jul 21, 2013 14:54
santhiago escreveu:Se não cometi nenhum equívoco com o raciocínio o módulo do vetor
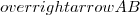
fornece a distância do ponto (1,1,1) ao plano de equação vide propriedade do conjunto S .Como só estamos queremos a soma das coordenadas do ponto A .Vamos verificar :

.
Escolhendo por exemplo

temos :
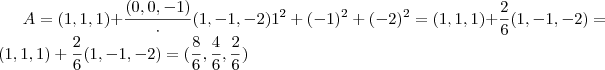
Logo ,

.
Certíssimo, consegui aplicar também aqui o sua ideia chegando na mesma resposta.. É um pouco trabalhosa, mas vale a pena se chegarmos no mesmo resultado.
Mas como já diz o ditado: Sem esforço não há recompensa. Mais uma vez, muito obrigado!
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por MateusL » Dom Jul 21, 2013 15:00
por MateusL » Dom Jul 21, 2013 15:00
O vetor normal ao plano

é

Temos que achar

tal que:

Ou seja, um valor de

tal que
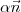
seja igual à projeção ortogonal de
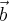
em relação a

, pois assim, e somente assim,
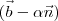
será ortogonal a

(em outras palavras, pertencerá a

), implicando que o produto escalar entre esses dois vetores seja igual a zero.
Achando

, o vetor procurado será

, que é a projeção de
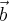
em

.
Abraço!
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [VETORES]Alguém me ajuda com vetores?
por LAZAROTTI » Seg Set 17, 2012 00:49
- 2 Respostas
- 7360 Exibições
- Última mensagem por young_jedi

Seg Set 17, 2012 11:28
Geometria Analítica
-
- [Vetores] Módulo e Versor de vetores
por LAZAROTTI » Sáb Set 22, 2012 22:42
- 1 Respostas
- 2988 Exibições
- Última mensagem por young_jedi

Sáb Set 22, 2012 22:50
Geometria Analítica
-
- [Vetores] Produto Entre Vetores
por _bruno94 » Qua Jul 10, 2013 00:34
- 1 Respostas
- 5205 Exibições
- Última mensagem por temujin

Qua Jul 10, 2013 14:27
Geometria Analítica
-
- [Vetores] Vetores iguais
por KleinIll » Dom Nov 04, 2012 12:17
- 2 Respostas
- 3397 Exibições
- Última mensagem por KleinIll

Dom Nov 04, 2012 13:50
Geometria Analítica
-
- [Vetores] Operações com vetores
por IlgssonBraga » Qui Jul 18, 2013 11:42
- 1 Respostas
- 2372 Exibições
- Última mensagem por Russman

Qui Jul 18, 2013 15:45
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 } e
} e 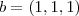 .
.

 } e
} e 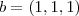 .
.

 do
do  ,mais precisamente ,
,mais precisamente ,  um é subespaço do
um é subespaço do  ,seus vetores são os pontos
,seus vetores são os pontos  que satisfaz a propriedade do conjunto
que satisfaz a propriedade do conjunto  que é
que é 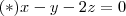 . Indo diretamente a geometria analítica ,seja
. Indo diretamente a geometria analítica ,seja 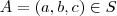 o ponto mais próximo de
o ponto mais próximo de  .Definindo
.Definindo  vetor normal ao plano que passa pela origem de equação
vetor normal ao plano que passa pela origem de equação  e escolhendo um ponto arbitrário
e escolhendo um ponto arbitrário  em
em  (Escolha o ponto que você quiser,fique à vontade !) .
(Escolha o ponto que você quiser,fique à vontade !) . 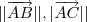 e hipotenusa
e hipotenusa  ,fica fácil ver as seguintes relações :
,fica fácil ver as seguintes relações : 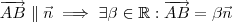

 .
.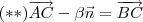 .Multiplicando-se escalarmente
.Multiplicando-se escalarmente  por
por  e usando (b) , segue :
e usando (b) , segue :  .
.  .
.  . Agora já conseguimos obter o ponto
. Agora já conseguimos obter o ponto  ,pois já temos o ponto
,pois já temos o ponto  ,o ponto
,o ponto  e o vetor
e o vetor  .Tente concluir .
.Tente concluir .
do
,mais precisamente ,
um é subespaço do
,seus vetores são os pontos
que satisfaz a propriedade do conjunto
que é
. Indo diretamente a geometria analítica ,seja
o ponto mais próximo de
.Definindo
vetor normal ao plano que passa pela origem de equação
e escolhendo um ponto arbitrário
em
(Escolha o ponto que você quiser,fique à vontade !) .
e hipotenusa
,fica fácil ver as seguintes relações :
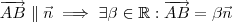

.
.Multiplicando-se escalarmente
por
e usando (b) , segue :
.
.
. Agora já conseguimos obter o ponto
,pois já temos o ponto
,o ponto
e o vetor
.Tente concluir .


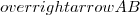 fornece a distância do ponto (1,1,1) ao plano de equação vide propriedade do conjunto S .Como só estamos queremos a soma das coordenadas do ponto A .Vamos verificar :
fornece a distância do ponto (1,1,1) ao plano de equação vide propriedade do conjunto S .Como só estamos queremos a soma das coordenadas do ponto A .Vamos verificar :  .
. temos :
temos : 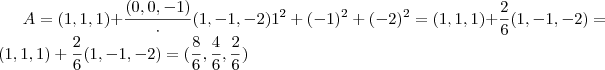
 .
.
fornece a distância do ponto (1,1,1) ao plano de equação vide propriedade do conjunto S .Como só estamos queremos a soma das coordenadas do ponto A .Vamos verificar :
.
temos :
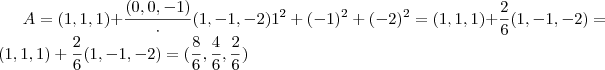
.

 é
é 
 tal que:
tal que:
 tal que
tal que 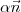 seja igual à projeção ortogonal de
seja igual à projeção ortogonal de 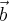 em relação a
em relação a  , pois assim, e somente assim,
, pois assim, e somente assim, 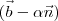 será ortogonal a
será ortogonal a  (em outras palavras, pertencerá a
(em outras palavras, pertencerá a  ), implicando que o produto escalar entre esses dois vetores seja igual a zero.
), implicando que o produto escalar entre esses dois vetores seja igual a zero. , o vetor procurado será
, o vetor procurado será  , que é a projeção de
, que é a projeção de 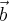 em
em  .
.





