




 em evidência na primeira equação ,temos :
em evidência na primeira equação ,temos : 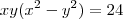 .Já na segunda equação manipulando ela de forma de conveniente de obtermos uma equação com os termos semelhantes com o da primeira ,segue que 2ª eq . é equivalente a :
.Já na segunda equação manipulando ela de forma de conveniente de obtermos uma equação com os termos semelhantes com o da primeira ,segue que 2ª eq . é equivalente a :  , multiplicando ambos lados por
, multiplicando ambos lados por 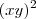 ,segue
,segue ![(a_1) \hspace{15mm} (xy[x^2-y^2] -2(xy)^2)(xy[x^2-y^2] +2(xy)^2) = 28(xy)^2 (a_1) \hspace{15mm} (xy[x^2-y^2] -2(xy)^2)(xy[x^2-y^2] +2(xy)^2) = 28(xy)^2](/latexrender/pictures/abf588dc3a46426fcd4313dc9a369d0f.png) .Comparando o item
.Comparando o item  com a equação 1 do sistema que você postou ,podemos substituir
com a equação 1 do sistema que você postou ,podemos substituir ![xy[x^2-y^2] xy[x^2-y^2]](/latexrender/pictures/90a6005c5a9b4e14687adc99f627c46e.png) por
por  ,logo
,logo 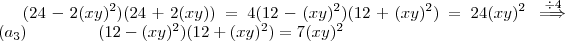 .
. ,temos :
,temos :  .Agora podemos resolver esta equação aplicando a fórmula resolvente ,
.Agora podemos resolver esta equação aplicando a fórmula resolvente , 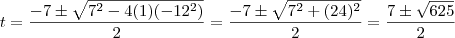 .Como
.Como  não é negativo ,a única possibilidade é :
não é negativo ,a única possibilidade é : 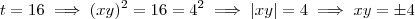 . Esta última relação ,permite substituir
. Esta última relação ,permite substituir 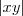 em
em 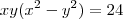 e além disso ,podemos escrever
e além disso ,podemos escrever  em função de
em função de  , e por fim vamos ter uma equação em apenas uma variável .Então :
, e por fim vamos ter uma equação em apenas uma variável .Então : 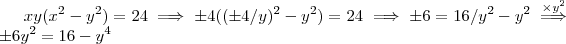 ;está equação pode ser resolvida de forma análoga a
;está equação pode ser resolvida de forma análoga a  . Encontrando
. Encontrando  ,basta lembrar que
,basta lembrar que  .
.  ,fica como exercício .Não estou vendo uma forma mais simples ,talvez há outras possibilidades ...
,fica como exercício .Não estou vendo uma forma mais simples ,talvez há outras possibilidades ...
 por bháskara o 7 está positivo ao invés de negativo ao final.
por bháskara o 7 está positivo ao invés de negativo ao final.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.