 por brunnkpol » Dom Jun 09, 2013 10:11
por brunnkpol » Dom Jun 09, 2013 10:11
Como posso resolver esse sistema? Não possuo esse conhecimento.

-
brunnkpol
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Ter Mai 07, 2013 16:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Dom Jun 09, 2013 13:05
por e8group » Dom Jun 09, 2013 13:05
Sistemas não lineares geralmente não são fáceis de ser resolvidos ,mas vamos tentar .
Deixando

em evidência na primeira equação ,temos :
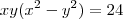
.Já na segunda equação manipulando ela de forma de conveniente de obtermos uma equação com os termos semelhantes com o da primeira ,segue que 2ª eq . é equivalente a :

, multiplicando ambos lados por
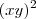
,segue
![(a_1) \hspace{15mm} (xy[x^2-y^2] -2(xy)^2)(xy[x^2-y^2] +2(xy)^2) = 28(xy)^2 (a_1) \hspace{15mm} (xy[x^2-y^2] -2(xy)^2)(xy[x^2-y^2] +2(xy)^2) = 28(xy)^2](/latexrender/pictures/abf588dc3a46426fcd4313dc9a369d0f.png)
.Comparando o item

com a equação 1 do sistema que você postou ,podemos substituir
![xy[x^2-y^2] xy[x^2-y^2]](/latexrender/pictures/90a6005c5a9b4e14687adc99f627c46e.png)
por

,logo
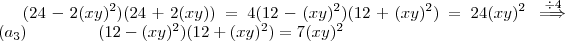
.
Fazendo

,temos :

.Agora podemos resolver esta equação aplicando a fórmula resolvente ,
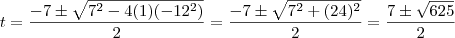
.Como

não é negativo ,a única possibilidade é :
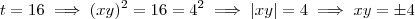
. Esta última relação ,permite substituir
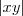
em
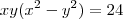
e além disso ,podemos escrever

em função de

, e por fim vamos ter uma equação em apenas uma variável .Então :
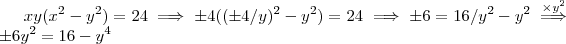
;está equação pode ser resolvida de forma análoga a

. Encontrando

,basta lembrar que

.
Observação :
Tente manipular a segunda equação e chegar em

,fica como exercício .Não estou vendo uma forma mais simples ,talvez há outras possibilidades ...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por brunnkpol » Ter Jun 11, 2013 00:43
por brunnkpol » Ter Jun 11, 2013 00:43
Obrigado por responder, consegui desenvolver por esse método o problema. Achava que tinha outro método que desconhecia, mas pelo que vi é uma questão de manipulação nas equações.
Só um detalhe, acho que na resolução da equação

por bháskara o 7 está positivo ao invés de negativo ao final.
-
brunnkpol
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Ter Mai 07, 2013 16:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4493 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- Sistema de equações
por Cleyson007 » Sex Set 12, 2008 12:47
- 6 Respostas
- 5533 Exibições
- Última mensagem por Cleyson007

Qua Jun 03, 2009 17:25
Sistemas de Equações
-
- Sistema de Equações
por Cleyson007 » Qua Mai 27, 2009 14:01
- 3 Respostas
- 3344 Exibições
- Última mensagem por Cleyson007

Qui Mai 28, 2009 17:51
Sistemas de Equações
-
- Sistema de equações
por Moreno1986 » Seg Mai 17, 2010 15:04
- 3 Respostas
- 3591 Exibições
- Última mensagem por Neperiano

Ter Mai 18, 2010 17:54
Sistemas de Equações
-
- Sistema de equações
por Moreno1986 » Sex Abr 23, 2010 13:54
- 1 Respostas
- 1554 Exibições
- Última mensagem por MarceloFantini

Sáb Abr 24, 2010 00:56
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 em evidência na primeira equação ,temos :
em evidência na primeira equação ,temos : 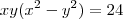 .Já na segunda equação manipulando ela de forma de conveniente de obtermos uma equação com os termos semelhantes com o da primeira ,segue que 2ª eq . é equivalente a :
.Já na segunda equação manipulando ela de forma de conveniente de obtermos uma equação com os termos semelhantes com o da primeira ,segue que 2ª eq . é equivalente a :  , multiplicando ambos lados por
, multiplicando ambos lados por 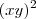 ,segue
,segue ![(a_1) \hspace{15mm} (xy[x^2-y^2] -2(xy)^2)(xy[x^2-y^2] +2(xy)^2) = 28(xy)^2 (a_1) \hspace{15mm} (xy[x^2-y^2] -2(xy)^2)(xy[x^2-y^2] +2(xy)^2) = 28(xy)^2](/latexrender/pictures/abf588dc3a46426fcd4313dc9a369d0f.png) .Comparando o item
.Comparando o item  com a equação 1 do sistema que você postou ,podemos substituir
com a equação 1 do sistema que você postou ,podemos substituir ![xy[x^2-y^2] xy[x^2-y^2]](/latexrender/pictures/90a6005c5a9b4e14687adc99f627c46e.png) por
por  ,logo
,logo 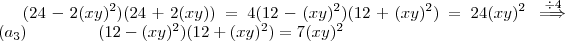 .
. ,temos :
,temos :  .Agora podemos resolver esta equação aplicando a fórmula resolvente ,
.Agora podemos resolver esta equação aplicando a fórmula resolvente , 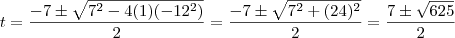 .Como
.Como  não é negativo ,a única possibilidade é :
não é negativo ,a única possibilidade é : 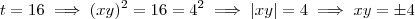 . Esta última relação ,permite substituir
. Esta última relação ,permite substituir 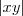 em
em 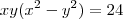 e além disso ,podemos escrever
e além disso ,podemos escrever  em função de
em função de  , e por fim vamos ter uma equação em apenas uma variável .Então :
, e por fim vamos ter uma equação em apenas uma variável .Então : 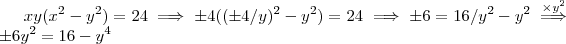 ;está equação pode ser resolvida de forma análoga a
;está equação pode ser resolvida de forma análoga a  . Encontrando
. Encontrando  ,basta lembrar que
,basta lembrar que  .
.  ,fica como exercício .Não estou vendo uma forma mais simples ,talvez há outras possibilidades ...
,fica como exercício .Não estou vendo uma forma mais simples ,talvez há outras possibilidades ...
 por bháskara o 7 está positivo ao invés de negativo ao final.
por bháskara o 7 está positivo ao invés de negativo ao final.





