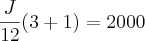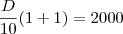UMA EMPRESA IRÁ DIVIDIR R$ 24.000,00 ENTRE 4 FUNCIONARIOS DE FORMA DIRETAMENTE PROPORCIONAL AO TEMPO DE TRABALAHO NA EMPRESA E INVERSAMENTE PROPORCIONAL AO NÚMERO DE FALTAS MAIS UM.QUANTO COUBE AO FUNCIONÁRIO MAIS ANTIGO,SABENDO QUE MARCOS TRABALHA HÁ 6 ANOS NA EMPRESA E FALTOU 2 VEZES,AURÉLIO TRABALHA 2 ANOS E NUNCA FALTOU,JOEL TRABALHA HÁ 12 ANOS E FALTOU 3 VEZES E DANIEL TRABALHA HÁ 10 ANOS E FALTOU APENAS UMA VEZ ?
eu resolvi esse problema da seguinte forma :
M + A+ J+ D = 24.000
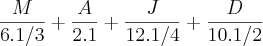 --- >
--- >
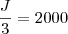
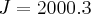

Existe outra forma para resolver esse problema ??? desde já agradeço xD



 (Onde 6 corresponde ao tempo de serviço e 3 corresponde ao n° de faltas + 1)
(Onde 6 corresponde ao tempo de serviço e 3 corresponde ao n° de faltas + 1)