 por virginia » Dom Jun 02, 2013 08:40
por virginia » Dom Jun 02, 2013 08:40
O preço de venda de um produto é de R$ 27,00. A venda de 100 unidades dá um lucro de R$ 260,00. Sabendo que o custo fixo de produção é de R$ 540,00 e que o custo variável é proporcional ao número de unidades produzidas, determine:
Não consegui desenvolver a questão da letra b tem a c, porém ainda não tentei elaborar.
a) A função receita total - essa eu fiz deu R(x)=27.x
b) O custo variável para uma produção de 2000 unidades
Eu fiz assim; 27x-24,40x = C(custo) - que deu c=2,6x , 2,6*2000=5200 mais a resposta não é esta e sim 38000??? Me ajudem
-
virginia
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Jul 12, 2012 15:15
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Administração
- Andamento: formado
 por virginia » Dom Jun 02, 2013 22:48
por virginia » Dom Jun 02, 2013 22:48
Muitíssimo obrigado. Consegui compreender e fiz a letra c sozinha. Valeu.
-
virginia
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Jul 12, 2012 15:15
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Administração
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Custo padrão e custo real] contabilidade
por Ederson_ederson » Seg Jan 16, 2017 14:38
- 0 Respostas
- 2057 Exibições
- Última mensagem por Ederson_ederson

Seg Jan 16, 2017 14:38
Matemática Financeira
-
- Custo de Produção
por gustavowelp » Seg Jul 18, 2011 00:05
- 3 Respostas
- 2694 Exibições
- Última mensagem por MarceloFantini

Seg Jul 18, 2011 12:58
Matemática Financeira
-
- [max e min] custo aquario
por Leandro Goncalves » Ter Abr 29, 2014 23:39
- 1 Respostas
- 4486 Exibições
- Última mensagem por Leandro Goncalves

Sex Mai 02, 2014 23:39
Equações
-
- [custo marginal] Problema
por Revelants » Dom Out 05, 2008 14:56
- 1 Respostas
- 3298 Exibições
- Última mensagem por admin

Ter Out 14, 2008 15:04
Matemática Financeira
-
- Função Custo Total
por Anderson_sa » Dom Mar 15, 2009 03:51
- 1 Respostas
- 7020 Exibições
- Última mensagem por Neperiano

Sáb Ago 20, 2011 22:46
Pedidos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


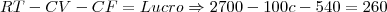

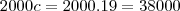



 , avisa que eu resolvo.
, avisa que eu resolvo.

