 por CBRJ » Ter Abr 09, 2013 23:51
por CBRJ » Ter Abr 09, 2013 23:51
Preciso escrever a forma genérica da função que expressaria o montante a cada mês de uma aplicação mensal constante, a uma taxa composta constante.
Aplicação inicial = R$ 100
Aplicação mensal = R$ 100
Taxa de juros (composta) = 0,7% a.m.
Ex: abr/13 = 100,00, mai/13 = 200,70, jun/13 = 302,10...
Já tentei utilizar somatório, mas não deu certo.
-
CBRJ
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Out 09, 2012 23:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por anabatista » Qua Abr 10, 2013 00:11
por anabatista » Qua Abr 10, 2013 00:11
Seguindo a regra de juros compostos temos
M

como o valor está acumulando com o do mês anterior,
voce utiliza
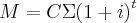
confere ai!
-
anabatista
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Abr 08, 2013 23:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatistica
- Andamento: cursando
 por CBRJ » Qua Abr 10, 2013 00:56
por CBRJ » Qua Abr 10, 2013 00:56
anabatista escreveu:Seguindo a regra de juros compostos temos
M

como o valor está acumulando com o do mês anterior,
voce utiliza
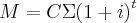
confere ai!
Fiz o teste até o 3º mês, deu um resultado diferente: R$ 304,20. Tem certeza que esse é o resultado certo?
-
CBRJ
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Out 09, 2012 23:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por anabatista » Qua Abr 10, 2013 01:06
por anabatista » Qua Abr 10, 2013 01:06
Cheque direitinho
fiz o teste ate o terceiro mês e ta bantendo
vamo la!
Abril como é o mês inicial, considera 0

Maio= 1
![M=100\left[ {(1+0,007)}^{0}+{(1+0,007)}^{1}\right]=200,7 M=100\left[ {(1+0,007)}^{0}+{(1+0,007)}^{1}\right]=200,7](/latexrender/pictures/9044840dca8915ea87fb03699fca09ba.png)
Junho=2
![M=100\left[ {(1+0,007)}^{0}+{(1+0,007)}^{1}+{(1+0,007)}^{2}\right]=302,10 M=100\left[ {(1+0,007)}^{0}+{(1+0,007)}^{1}+{(1+0,007)}^{2}\right]=302,10](/latexrender/pictures/9c2e0e36497defc2f9fb2d283f103560.png)
E por ai vai...
-
anabatista
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Abr 08, 2013 23:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatistica
- Andamento: cursando
 por CBRJ » Qua Abr 10, 2013 01:36
por CBRJ » Qua Abr 10, 2013 01:36
Certo, é isso mesmo! Obrigado!!
-
CBRJ
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Out 09, 2012 23:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Aplicação de Função Exponencial
por Bruhh » Seg Mar 22, 2010 16:47
- 1 Respostas
- 3638 Exibições
- Última mensagem por Elcioschin

Seg Mar 22, 2010 19:10
Funções
-
- [Função diferenciável] Aplicação de planos tangentes
por willlol01 » Sex Mai 06, 2016 22:28
- 1 Respostas
- 2612 Exibições
- Última mensagem por adauto martins

Sáb Mai 14, 2016 15:43
Cálculo: Limites, Derivadas e Integrais
-
- Variação Constante
por Andreza » Ter Fev 28, 2012 19:04
- 2 Respostas
- 2450 Exibições
- Última mensagem por MarceloFantini

Ter Fev 28, 2012 21:53
Funções
-
- calcular constante no limite
por uefs » Qui Abr 17, 2014 00:23
- 8 Respostas
- 4722 Exibições
- Última mensagem por e8group

Sáb Abr 19, 2014 21:24
Cálculo: Limites, Derivadas e Integrais
-
- duvida - derivada de constante
por hallory03 » Dom Jun 22, 2014 16:42
- 2 Respostas
- 1966 Exibições
- Última mensagem por hallory03

Qui Jun 26, 2014 17:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



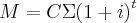

![M=100\left[ {(1+0,007)}^{0}+{(1+0,007)}^{1}\right]=200,7 M=100\left[ {(1+0,007)}^{0}+{(1+0,007)}^{1}\right]=200,7](/latexrender/pictures/9044840dca8915ea87fb03699fca09ba.png)
![M=100\left[ {(1+0,007)}^{0}+{(1+0,007)}^{1}+{(1+0,007)}^{2}\right]=302,10 M=100\left[ {(1+0,007)}^{0}+{(1+0,007)}^{1}+{(1+0,007)}^{2}\right]=302,10](/latexrender/pictures/9c2e0e36497defc2f9fb2d283f103560.png)
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
