 por Myneyrynho » Ter Mar 19, 2013 15:09
por Myneyrynho » Ter Mar 19, 2013 15:09
Uma máquina de lavar sofreu duas variações sucessivas de x% e 9%, sendo vendida hoje por 1.030,05. Se antes das duas valorizações a máquina era vendida por 900,00, calcule porcentual x.
Então vamos lá...
Pi(Preço inicial)= 900,00
Pf(Preço final)= 1030,05
1º Variação = x%
2º Variação = 9%
i = variação
Então fiz assim:
Pf=Pi (1+i)(1+i)
1030,05 = 900 (1 + x)(1 + 0,9)
1030,05 = 900 (1x)(1,09)
1030,05 = 981x
x = 1030,05/981
x = 1,05
Então a taxa "x" é 5% ?
Estou na duvida... ajudem por favor.
-
Myneyrynho
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sáb Mar 16, 2013 12:15
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por nakagumahissao » Ter Mar 19, 2013 16:42
por nakagumahissao » Ter Mar 19, 2013 16:42
Veja bem Myneyrynho,
Na questão não foi levantada a hipótese de acréscimo percentual, porém, sendo que o valor inicial foi de 900,00 e se tornou 1030,05, podemos supor que sim e desta maneira, sua resposta (5%) está correta.
Porém há outra maneira de ser interpretada:
Sejam x a primeira taxa em %, 9%=0,09 a segunda taxa sucessiva, C = 900,00 e V = 1030,05, tem-se desta maneira:
0,09.C.x = 1030,05 = (0,09)(900)x = 1030,05 => x = 1030,05 / 81 => x = 12,7167%
Acredito que sua resposta é a correta neste caso, mas a questão é ambígua.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por Myneyrynho » Ter Mar 19, 2013 17:30
por Myneyrynho » Ter Mar 19, 2013 17:30
Agora to mais confuso ...
como se trata de acréscimos sucessivos:
temos o valor inicial de 900 que sofre acréscimos de x% e esse valos sofre acréscimos de 7%...
Se eu substituir o "x" por 5 igual eu aparentemente achei... fazendo as contas dos 2 acréscimos chegaria a 1011,15
Ou seja, creio que está errado =x
Agora me peri todo ;x
-
Myneyrynho
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sáb Mar 16, 2013 12:15
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por nakagumahissao » Ter Mar 19, 2013 18:16
por nakagumahissao » Ter Mar 19, 2013 18:16
Myneyrynho,
Seria da seguinte forma:
900 x (1 + 0,05) x (1 + 0,09) = 900 x 1,05 x 1,09 = 1030,05
Ou seja,
Parte (1) = 900 x 0,05 = 45
Valor Acumulado (1) = 900 + 45 = 945
Parte (2) = 945 x 0,09 = 85,05
Valor Acumulado (2) = Valor Acumulado (1) + Parte (2) = 945 + 85,05 = 1030,05
Quando acrescentamos 1 à porcentagem, estamos calculando o valor acumulado. Desta maneira, 1 + 0,09 implica em dizermos que estamos acrescentando 9% ao valor montante. Para darmos um desconto de 9% por exemplo, seria o contrário, ou seja, 1 - 0,09! (Escrevi sobre isso algum tempo atrás =
http://learning.freeiz.com/2013/03/11/descontos-e-acrescimos-percentuais/)
Espero ter ajudado
Editado pela última vez por
nakagumahissao em Ter Mar 19, 2013 18:32, em um total de 1 vez.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por nakagumahissao » Ter Mar 19, 2013 18:23
por nakagumahissao » Ter Mar 19, 2013 18:23
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [porcentagem] duvida neste exercicio, uma ajudinha vai bem.
por charlesromulo33 » Seg Jan 19, 2015 15:22
- 2 Respostas
- 2278 Exibições
- Última mensagem por charlesromulo33

Sex Jan 23, 2015 07:47
Matemática Financeira
-
- [Porcentagem] Fração mista e porcentagem
por Mayra Luna » Ter Fev 26, 2013 20:58
- 2 Respostas
- 4572 Exibições
- Última mensagem por Mayra Luna

Ter Fev 26, 2013 23:41
Álgebra Elementar
-
- Resolva em R
por andersontricordiano » Dom Fev 16, 2014 15:07
- 1 Respostas
- 1689 Exibições
- Última mensagem por young_jedi

Dom Fev 16, 2014 20:26
Logaritmos
-
- [RESOLVA EM IR]
por mayconlucas » Seg Nov 09, 2015 10:16
- 0 Respostas
- 1296 Exibições
- Última mensagem por mayconlucas

Seg Nov 09, 2015 10:16
Álgebra Elementar
-
- [RESOLVA EM IR]
por mayconlucas » Seg Nov 09, 2015 10:13
- 1 Respostas
- 1309 Exibições
- Última mensagem por nakagumahissao

Ter Nov 10, 2015 08:56
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



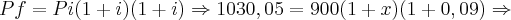
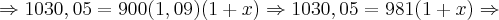
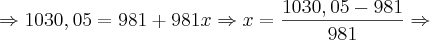

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.