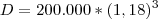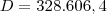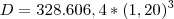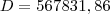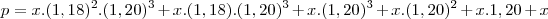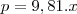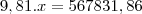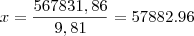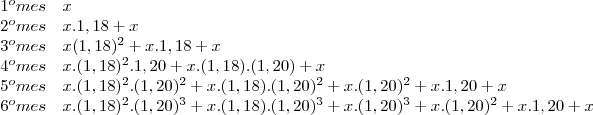Gente me socorre, ja tentei de todos os jeitos.
Calcular o valor das prestações mensais, iguais, consecutivas e postecipadas que
liquidam um débito de R$ 200.000 no prazo de 6 meses, sendo a taxa de juros efetiva de
18%am para os três primeiros meses, e de 20%am para os demais.
Resp. PV = R$ 200.000, i 1-3 = 18%am, i 4-6 = 20%am, então PMT post = R$ 57864,73
Já fiz deste modos:
PMT: PV . i / 1-(1+i)^-n
aí fiz assim:
PMT: [200.000*0,18/ 1-(1+0,18)^-6] +[ 200.000*0,20/1-(1+0,20)^-6]
aí tentei assim:
PMT: PV/(1+i)^-1 + (1+i)^-2+ (1+i)^-3+ (1+i)^-4+ (1+i)^-5+(1+i)^-6
PMT: 200.000/(1+0,18)^-1 + (1+0,18)^-2+ (1+0,18)^-3+ (1+0,20)^-4+ (1+0,20)^-5+(1+0,20)^-6
Mas nenhum dá!!!