É uma dúvida antiga que achei nos meus apontamentos.
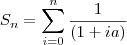
Grato pela atenção.

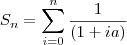

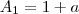



 . Assim , teremos que :
. Assim , teremos que :

 , poderíamos dizer que
, poderíamos dizer que 

 ? Existe alguma informação a respeito dele, como por exemplo se
? Existe alguma informação a respeito dele, como por exemplo se 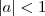 ? Ou
? Ou  ? Claramente
? Claramente 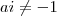 por condições de existência, mas parece pouco.
por condições de existência, mas parece pouco. .
.

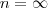 .
.  é uma constante. As restrições fazem parte da questão, mas se ajudar podemos considera-la maior que zero.
é uma constante. As restrições fazem parte da questão, mas se ajudar podemos considera-la maior que zero.
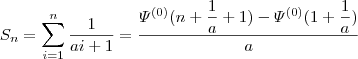
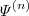 é a n-ésima derivada da função Digamma
é a n-ésima derivada da função Digamma
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante