Boa noite!
estou com um problema para tirar a indeterminacao em um serie e Fourier, ja jeguei nessa somatoria com + 1/pi mas nao consigo passar para n2
para poder chegar nessa outra resposta.



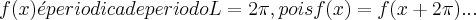 ...logo pode ser expandida em uma serie de fourier...
...logo pode ser expandida em uma serie de fourier...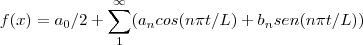 ...onde
...onde  ...logo,
...logo, =
= ...onde...
...onde... ...
...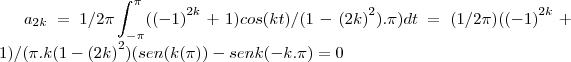 ...
... =
=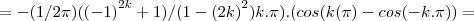
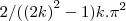 ...logo...
...logo...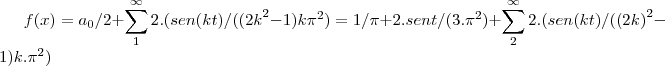 ...
...
 ...f(x) é uma funçao par,pois depende do cosseno...entao...
...f(x) é uma funçao par,pois depende do cosseno...entao...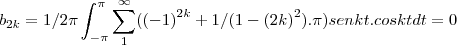 ,pois senkt é impar e coskt é par,logo o produto sera impar,e a integral de uma funçao impar em intervalo simetrico é zero...
,pois senkt é impar e coskt é par,logo o produto sera impar,e a integral de uma funçao impar em intervalo simetrico é zero...![{a}_{2k}=1/2\pi\int_{-\pi}^{\pi}\sum_{1}^{\infty}({-1}^{2k}+1/(1-{2k}^{2}.\pi)coskt.coskt dt=1/2\sum_{1}^{\infty}\int_{-\pi}^{\pi}(2/(1-{(2k)}^{2}.\pi){(coskt)}^{2}dt=1/2\sum_{1}^{\infty}(2/(1-{(2k)}^{2}.\pi)\int_{0}^{2 \pi}{(coskt)}^{2}dt=1/\pi\sum_{1}^{\infty}(1/(1-{(2k)}^{2}).\pi(senkt.coskt/k)[\pi,-\pi]+1/2\int_{0}^{2\pi}dt= {a}_{2k}=1/2\pi\int_{-\pi}^{\pi}\sum_{1}^{\infty}({-1}^{2k}+1/(1-{2k}^{2}.\pi)coskt.coskt dt=1/2\sum_{1}^{\infty}\int_{-\pi}^{\pi}(2/(1-{(2k)}^{2}.\pi){(coskt)}^{2}dt=1/2\sum_{1}^{\infty}(2/(1-{(2k)}^{2}.\pi)\int_{0}^{2 \pi}{(coskt)}^{2}dt=1/\pi\sum_{1}^{\infty}(1/(1-{(2k)}^{2}).\pi(senkt.coskt/k)[\pi,-\pi]+1/2\int_{0}^{2\pi}dt=](/latexrender/pictures/d7a8f1551b0250f40d9d82bd32da02ff.png)


Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)