 por Nelio F Junior » Seg Nov 02, 2015 22:18
por Nelio F Junior » Seg Nov 02, 2015 22:18
Boa noite!
estou com um problema para tirar a indeterminacao em um serie e Fourier, ja jeguei nessa somatoria com + 1/pi mas nao consigo passar para n2
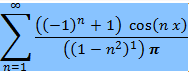
- somatoria.png (2 KiB) Exibido 4087 vezes
para poder chegar nessa outra resposta.
-
Nelio F Junior
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Nov 02, 2015 22:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng Mecatrônica
- Andamento: cursando
 por adauto martins » Sex Nov 06, 2015 18:27
por adauto martins » Sex Nov 06, 2015 18:27
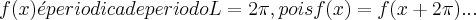
...logo pode ser expandida em uma serie de fourier...
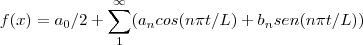
...onde

...logo,

=

...onde...

...
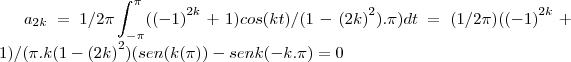
...

=
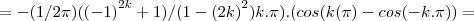
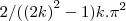
...logo...
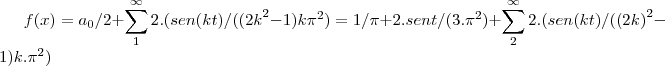
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Dom Nov 08, 2015 12:22
por adauto martins » Dom Nov 08, 2015 12:22
uma correçao...
errei no calculo dos

...f(x) é uma funçao par,pois depende do cosseno...entao...
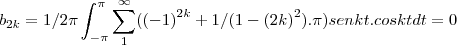
,pois senkt é impar e coskt é par,logo o produto sera impar,e a integral de uma funçao impar em intervalo simetrico é zero...
![{a}_{2k}=1/2\pi\int_{-\pi}^{\pi}\sum_{1}^{\infty}({-1}^{2k}+1/(1-{2k}^{2}.\pi)coskt.coskt dt=1/2\sum_{1}^{\infty}\int_{-\pi}^{\pi}(2/(1-{(2k)}^{2}.\pi){(coskt)}^{2}dt=1/2\sum_{1}^{\infty}(2/(1-{(2k)}^{2}.\pi)\int_{0}^{2 \pi}{(coskt)}^{2}dt=1/\pi\sum_{1}^{\infty}(1/(1-{(2k)}^{2}).\pi(senkt.coskt/k)[\pi,-\pi]+1/2\int_{0}^{2\pi}dt= {a}_{2k}=1/2\pi\int_{-\pi}^{\pi}\sum_{1}^{\infty}({-1}^{2k}+1/(1-{2k}^{2}.\pi)coskt.coskt dt=1/2\sum_{1}^{\infty}\int_{-\pi}^{\pi}(2/(1-{(2k)}^{2}.\pi){(coskt)}^{2}dt=1/2\sum_{1}^{\infty}(2/(1-{(2k)}^{2}.\pi)\int_{0}^{2 \pi}{(coskt)}^{2}dt=1/\pi\sum_{1}^{\infty}(1/(1-{(2k)}^{2}).\pi(senkt.coskt/k)[\pi,-\pi]+1/2\int_{0}^{2\pi}dt=](/latexrender/pictures/d7a8f1551b0250f40d9d82bd32da02ff.png)

-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como resolver esta indeterminação?
por joaofonseca » Qui Mar 22, 2012 14:57
- 2 Respostas
- 3455 Exibições
- Última mensagem por joaofonseca

Qui Mar 22, 2012 18:37
Cálculo: Limites, Derivadas e Integrais
-
- Expressões, me ajudem a tirar esta duvida
por teilom » Dom Ago 12, 2012 17:15
- 1 Respostas
- 1410 Exibições
- Última mensagem por MarceloFantini

Dom Ago 12, 2012 18:24
Álgebra Elementar
-
- 8/0+32-16/0 = 32 ou é uma indeterminação?
por Therodrigou » Dom Jun 24, 2018 16:44
- 4 Respostas
- 10725 Exibições
- Última mensagem por DanielFerreira

Dom Jul 08, 2018 16:12
Álgebra
-
- Indeterminação?
por Rafael16 » Qui Jun 20, 2013 13:36
- 2 Respostas
- 2037 Exibições
- Última mensagem por Rafael16

Qui Jun 20, 2013 14:52
Cálculo: Limites, Derivadas e Integrais
-
- Levantar indeterminação
por Marcampucio » Ter Mar 10, 2009 18:02
- 2 Respostas
- 4393 Exibições
- Última mensagem por Marcampucio

Qua Mar 11, 2009 21:04
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



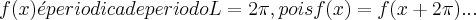 ...logo pode ser expandida em uma serie de fourier...
...logo pode ser expandida em uma serie de fourier...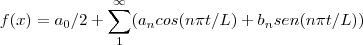 ...onde
...onde  ...logo,
...logo, =
= ...onde...
...onde... ...
...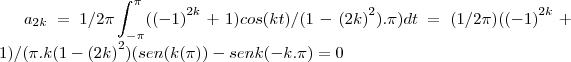 ...
... =
=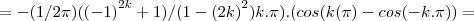
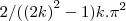 ...logo...
...logo...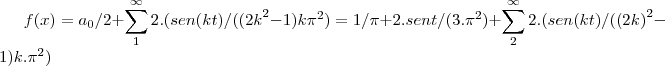 ...
...
 ...f(x) é uma funçao par,pois depende do cosseno...entao...
...f(x) é uma funçao par,pois depende do cosseno...entao...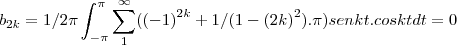 ,pois senkt é impar e coskt é par,logo o produto sera impar,e a integral de uma funçao impar em intervalo simetrico é zero...
,pois senkt é impar e coskt é par,logo o produto sera impar,e a integral de uma funçao impar em intervalo simetrico é zero...![{a}_{2k}=1/2\pi\int_{-\pi}^{\pi}\sum_{1}^{\infty}({-1}^{2k}+1/(1-{2k}^{2}.\pi)coskt.coskt dt=1/2\sum_{1}^{\infty}\int_{-\pi}^{\pi}(2/(1-{(2k)}^{2}.\pi){(coskt)}^{2}dt=1/2\sum_{1}^{\infty}(2/(1-{(2k)}^{2}.\pi)\int_{0}^{2 \pi}{(coskt)}^{2}dt=1/\pi\sum_{1}^{\infty}(1/(1-{(2k)}^{2}).\pi(senkt.coskt/k)[\pi,-\pi]+1/2\int_{0}^{2\pi}dt= {a}_{2k}=1/2\pi\int_{-\pi}^{\pi}\sum_{1}^{\infty}({-1}^{2k}+1/(1-{2k}^{2}.\pi)coskt.coskt dt=1/2\sum_{1}^{\infty}\int_{-\pi}^{\pi}(2/(1-{(2k)}^{2}.\pi){(coskt)}^{2}dt=1/2\sum_{1}^{\infty}(2/(1-{(2k)}^{2}.\pi)\int_{0}^{2 \pi}{(coskt)}^{2}dt=1/\pi\sum_{1}^{\infty}(1/(1-{(2k)}^{2}).\pi(senkt.coskt/k)[\pi,-\pi]+1/2\int_{0}^{2\pi}dt=](/latexrender/pictures/d7a8f1551b0250f40d9d82bd32da02ff.png)

