
Sempre o somatório de n=1 até infinito.
Obrigado



 , para todo n) .
, para todo n) .  fixado , sempre
fixado , sempre  para
para  suficientemente grande .
suficientemente grande .  e comparar a série
e comparar a série 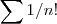 com a geométrica \sum (1/a)^n [/tex] .
com a geométrica \sum (1/a)^n [/tex] .

 , isto automaticamente implica
, isto automaticamente implica 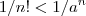 (em geral para n suficientemente grande , entretanto , para caso particulares , como
(em geral para n suficientemente grande , entretanto , para caso particulares , como  por exemplo .Neste caso basta impor que
por exemplo .Neste caso basta impor que 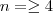 ) .
) .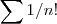 converge
converge  também converge .
também converge .
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: