Usando a propriedade arquimediana, prove que se
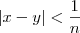 para todo
para todo 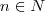 , então
, então 

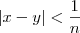 para todo
para todo 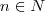 , então
, então 

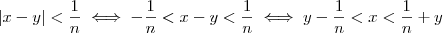
 o que é sempre verdade para qualquer
o que é sempre verdade para qualquer  real e nada concluímos.
real e nada concluímos. então ficaremos com
então ficaremos com  e portanto
e portanto  .
.
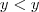 não faz muito sentido.
não faz muito sentido.


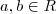 tais que
tais que  então existe algum
então existe algum  tal que
tal que 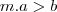 .
. , invertendo ficamos com
, invertendo ficamos com 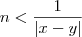 .
.  tal que
tal que  .
. em (3) só existirá se
em (3) só existirá se 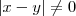

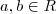 tais que
tais que  então existe algum
então existe algum  tal que
tal que 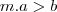 .
. . Vamos supor então que
. Vamos supor então que  e portanto
e portanto  .
. tal que
tal que  .
. então
então  também, chamemos esse produto de
também, chamemos esse produto de  .
. e
e 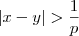 . Ambos
. Ambos  e
e  naturais quaisquer contrariando a hipótese dada no enunciado original e a nossa suposição de que
naturais quaisquer contrariando a hipótese dada no enunciado original e a nossa suposição de que  .
. .
.  } é igual a 0 (usando a Arquimediana). E daí usaríamos limites, mas aí estaríamos usando outros recursos além da Arquimediana.
} é igual a 0 (usando a Arquimediana). E daí usaríamos limites, mas aí estaríamos usando outros recursos além da Arquimediana.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)