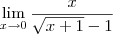
Não podemos aplicar a definição direta de limite, pois se substituirmos x por zero, teremos o denominador igual a zero.
Então racionalizando o denominador temos:
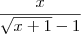 .
.  =
==
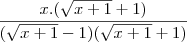 =
==
 =
==
 =
=Então:
=
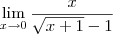 =
= =
 =
= 
Gostaria que alguem verificasse a minha resolução.



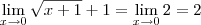 . Você aplicou o limite na primeira igualdade e manteve o limite, isto está errado. Deveria ter escrito
. Você aplicou o limite na primeira igualdade e manteve o limite, isto está errado. Deveria ter escrito 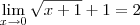 .
.

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)