[Limite]no Ponto Dado

por **eli83** » Sáb Out 06, 2012 14:16

Aplicando o conceito de exitência de limite, verifique se existe o limite da seguinte função quando x tende para zero:

$f(x)\ =\frac {\sqrt{5x^3 + 18}} {x+\frac{3}{2}}$

O limite de uma função existe, em dado ponto, quando existirem os limites laterais (no ponto dado) pela direita e pela esquerda, e os mesmos forem iguais. Mas eu não consegui fazer utilizando limites laterais.

Então fiz utilizando Continuidade.
Se f é contínua em a, então as três condições deverão ser satisfeitas.

existe f(a)

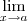
existe $\lim_{x\to a}$

$\lim_{x\to a}\ f(x) = f(a)$

Devemos verificar se:

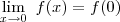
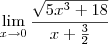$\lim_{x\to 0}\ f(x) = f(0)$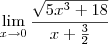

$\lim_{x\to 0}\frac {\sqrt{5x^3 + 18}} {x+\frac{3}{2}}$ = f(0)

$\lim_{x\to 0}\frac {\sqrt{5x^3 + 18}} {x+\frac{3}{2}}$

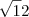
$\lim_{x\to 0} {\sqrt12}$ = ${\sqrt12}$

f(0) = ${\sqrt12}$

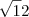
Portanto a função é continua no ponto x = 0

e também existe $\lim_{x\to 0}\frac {\sqrt{5x^3 + 18}} {x+\frac{3}{2}}$

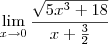
Gostaria de saber se esta resolução por continuidade está correta ou se eu devo usar limites laterais.

por **MarceloFantini** » Sáb Out 06, 2012 14:33

Você deve calculá-los separadamente para depois dizer que são iguais. Se você escrever $\lim_{x \to 0} \frac{\sqrt{5x^3 +18}}{x + \frac{3}{2}} = f(0)$ de cara você está afirmando o que quer provar e assim pode ter sua nota integralmente anulada.

Diga que não há qualquer restrições ao valor x=0

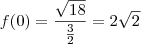e que $f(0) = \frac{\sqrt{18}}{\frac{3}{2}} = 2 \sqrt{2}$ . Por outro lado, calcule o limite e mostre que tem o mesmo valor. Logo eles existem e são iguais.

[Limite]no Ponto Dado

[Limite]no Ponto Dado

[Limite]no Ponto Dado

Re: [Limite]no Ponto Dado

Quem está online