 por giboia90 » Dom Ago 19, 2012 17:41
por giboia90 » Dom Ago 19, 2012 17:41
gostaria que detalhasse esse o segundo passo do limite.
![\lim_{x\rightarrow \infty }\left[ \sqrt[]{x + \sqrt[]{x + \sqrt[]{x}}} - \sqrt[]{x}\right] \lim_{x\rightarrow \infty }\left[ \sqrt[]{x + \sqrt[]{x + \sqrt[]{x}}} - \sqrt[]{x}\right]](/latexrender/pictures/9e5c38e7f06f9be9db74c8bb24672324.png)
eo segundo passo
![\lim_{x\rightarrow\infty}\frac{\sqrt[]{x}{\left(1+\frac{1}{\sqrt[]{x}} \right)}^{\frac{1}{2}}}{\sqrt[]{x}\left[ {\left(1+\frac{1}{\sqrt[]{x}} \sqrt[]{1+\frac{1}{\sqrt[]{x}}}\right)}^{\frac{1}{2}}+1\right]} \lim_{x\rightarrow\infty}\frac{\sqrt[]{x}{\left(1+\frac{1}{\sqrt[]{x}} \right)}^{\frac{1}{2}}}{\sqrt[]{x}\left[ {\left(1+\frac{1}{\sqrt[]{x}} \sqrt[]{1+\frac{1}{\sqrt[]{x}}}\right)}^{\frac{1}{2}}+1\right]}](/latexrender/pictures/edef6e6e811262c7345d64a4dc2bb831.png)
-
giboia90
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Dom Dez 04, 2011 01:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engeharia civil
- Andamento: cursando
 por MarceloFantini » Dom Ago 19, 2012 20:46
por MarceloFantini » Dom Ago 19, 2012 20:46
Não entendo o que você gostaria de esclarecer. O segundo limite que escreveu é o segundo passo que você quer entender?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por giboia90 » Dom Ago 19, 2012 21:16
por giboia90 » Dom Ago 19, 2012 21:16
sim são o mesmo limite, so queria saber como chega ao segundo passo e como:
![\sqrt[]{x+\sqrt[]{x}} = \sqrt[]{x}{\left(1+ \frac{1}{\sqrt[]{x}} \right)}^{\frac{1}{2}} \sqrt[]{x+\sqrt[]{x}} = \sqrt[]{x}{\left(1+ \frac{1}{\sqrt[]{x}} \right)}^{\frac{1}{2}}](/latexrender/pictures/3d2cdcae836c0f4345e8a0b10167aba5.png)
-
giboia90
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Dom Dez 04, 2011 01:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engeharia civil
- Andamento: cursando
 por MarceloFantini » Dom Ago 19, 2012 22:49
por MarceloFantini » Dom Ago 19, 2012 22:49
Note que

, daí

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por giboia90 » Dom Ago 19, 2012 23:07
por giboia90 » Dom Ago 19, 2012 23:07
mas como
![\sqrt[]{x}= x\left(\frac{1}{\sqrt[]{x}} \right) \sqrt[]{x}= x\left(\frac{1}{\sqrt[]{x}} \right)](/latexrender/pictures/04d55e82d4bba4c4b0130ef5bd8e9100.png)
-
giboia90
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Dom Dez 04, 2011 01:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engeharia civil
- Andamento: cursando
 por MarceloFantini » Seg Ago 20, 2012 14:09
por MarceloFantini » Seg Ago 20, 2012 14:09
Note que
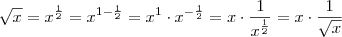
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Preciso entender como deu esse resultado!
por Adrielly » Qui Fev 11, 2010 11:26
- 4 Respostas
- 2353 Exibições
- Última mensagem por rojantsch

Sex Fev 19, 2010 12:56
Álgebra Elementar
-
- [FATORAÇÃO] como chegar no resultado final
por carolinaln » Seg Mai 08, 2017 20:46
- 1 Respostas
- 1965 Exibições
- Última mensagem por DanielFerreira

Dom Mai 14, 2017 00:51
Equações
-
- [Rodovia] - Quem chega primeiro
por NLAA » Qui Mar 15, 2018 20:52
- 0 Respostas
- 2164 Exibições
- Última mensagem por NLAA

Qui Mar 15, 2018 20:52
Aritmética
-
- resultado diferente - PG
por jose henrique » Qui Set 30, 2010 23:50
- 4 Respostas
- 3206 Exibições
- Última mensagem por MarceloFantini

Ter Out 05, 2010 01:18
Progressões
-
- Confirmação de resultado
por Fabiim » Seg Mai 09, 2011 22:19
- 2 Respostas
- 2903 Exibições
- Última mensagem por Fabiim

Qua Mai 11, 2011 20:49
Binômio de Newton
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow \infty }\left[ \sqrt[]{x + \sqrt[]{x + \sqrt[]{x}}} - \sqrt[]{x}\right] \lim_{x\rightarrow \infty }\left[ \sqrt[]{x + \sqrt[]{x + \sqrt[]{x}}} - \sqrt[]{x}\right]](/latexrender/pictures/9e5c38e7f06f9be9db74c8bb24672324.png)
![\lim_{x\rightarrow\infty}\frac{\sqrt[]{x}{\left(1+\frac{1}{\sqrt[]{x}} \right)}^{\frac{1}{2}}}{\sqrt[]{x}\left[ {\left(1+\frac{1}{\sqrt[]{x}} \sqrt[]{1+\frac{1}{\sqrt[]{x}}}\right)}^{\frac{1}{2}}+1\right]} \lim_{x\rightarrow\infty}\frac{\sqrt[]{x}{\left(1+\frac{1}{\sqrt[]{x}} \right)}^{\frac{1}{2}}}{\sqrt[]{x}\left[ {\left(1+\frac{1}{\sqrt[]{x}} \sqrt[]{1+\frac{1}{\sqrt[]{x}}}\right)}^{\frac{1}{2}}+1\right]}](/latexrender/pictures/edef6e6e811262c7345d64a4dc2bb831.png)

![\lim_{x\rightarrow \infty }\left[ \sqrt[]{x + \sqrt[]{x + \sqrt[]{x}}} - \sqrt[]{x}\right] \lim_{x\rightarrow \infty }\left[ \sqrt[]{x + \sqrt[]{x + \sqrt[]{x}}} - \sqrt[]{x}\right]](/latexrender/pictures/9e5c38e7f06f9be9db74c8bb24672324.png)
![\lim_{x\rightarrow\infty}\frac{\sqrt[]{x}{\left(1+\frac{1}{\sqrt[]{x}} \right)}^{\frac{1}{2}}}{\sqrt[]{x}\left[ {\left(1+\frac{1}{\sqrt[]{x}} \sqrt[]{1+\frac{1}{\sqrt[]{x}}}\right)}^{\frac{1}{2}}+1\right]} \lim_{x\rightarrow\infty}\frac{\sqrt[]{x}{\left(1+\frac{1}{\sqrt[]{x}} \right)}^{\frac{1}{2}}}{\sqrt[]{x}\left[ {\left(1+\frac{1}{\sqrt[]{x}} \sqrt[]{1+\frac{1}{\sqrt[]{x}}}\right)}^{\frac{1}{2}}+1\right]}](/latexrender/pictures/edef6e6e811262c7345d64a4dc2bb831.png)



![\sqrt[]{x+\sqrt[]{x}} = \sqrt[]{x}{\left(1+ \frac{1}{\sqrt[]{x}} \right)}^{\frac{1}{2}} \sqrt[]{x+\sqrt[]{x}} = \sqrt[]{x}{\left(1+ \frac{1}{\sqrt[]{x}} \right)}^{\frac{1}{2}}](/latexrender/pictures/3d2cdcae836c0f4345e8a0b10167aba5.png)


![\sqrt[]{x}= x\left(\frac{1}{\sqrt[]{x}} \right) \sqrt[]{x}= x\left(\frac{1}{\sqrt[]{x}} \right)](/latexrender/pictures/04d55e82d4bba4c4b0130ef5bd8e9100.png)

