 por citadp » Qua Jun 20, 2012 11:42
por citadp » Qua Jun 20, 2012 11:42
quando diz estude os extremos de uma função sem darem um intervalo ou ponto, basta calcular os zeros da derivada e ver onde são esses zeros?
Ou como se faz ?
Na função

dizem-me para calcular em IR, só calculo com os zeros da derivada ?
-
citadp
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Jun 02, 2012 13:11
- Formação Escolar: SUPLETIVO
- Área/Curso: Informática
- Andamento: cursando
 por e8group » Qua Jun 20, 2012 13:17
por e8group » Qua Jun 20, 2012 13:17
Seja g uma função ,onde
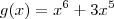
.Para estudarmos o extremos desta função, basta descobrir os pontos críticos de
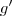
e analisa-os .

.
pontos críticos :

.
Teste da derivada segunda :
em

não podemos afirmar nada ,entretanto quando
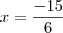
g tem um ponto de mínimo (neste caso global veja a figura abaixo em anexo ) pois ,
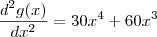
e portanto
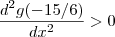
o que significa que há um ponto de mínimo .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [calculo] extremos;ponto de minimo e maximo
por beel » Dom Out 30, 2011 19:15
- 2 Respostas
- 2144 Exibições
- Última mensagem por LuizAquino

Seg Out 31, 2011 14:54
Cálculo: Limites, Derivadas e Integrais
-
- Ponto Máximo e Mínimo de uma função.
por lucasowner » Qui Ago 13, 2015 03:05
- 1 Respostas
- 2008 Exibições
- Última mensagem por nakagumahissao

Qui Ago 13, 2015 15:29
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] Ponto minimo/máximo e concavidade
por gabriel feron » Dom Out 07, 2012 03:52
- 1 Respostas
- 2202 Exibições
- Última mensagem por young_jedi

Dom Out 07, 2012 10:56
Cálculo: Limites, Derivadas e Integrais
-
- Questão de Máximo e Mínimo Global - Calculo I
por Mai96 » Qua Jul 08, 2015 22:12
- 2 Respostas
- 1744 Exibições
- Última mensagem por adauto martins

Qui Jul 16, 2015 18:39
Cálculo: Limites, Derivadas e Integrais
-
- Máximo e mínimo
por thadeu » Qua Nov 18, 2009 13:47
- 1 Respostas
- 4165 Exibições
- Última mensagem por Elcioschin

Qua Nov 18, 2009 17:50
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 dizem-me para calcular em IR, só calculo com os zeros da derivada ?
dizem-me para calcular em IR, só calculo com os zeros da derivada ?
 dizem-me para calcular em IR, só calculo com os zeros da derivada ?
dizem-me para calcular em IR, só calculo com os zeros da derivada ?
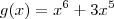 .Para estudarmos o extremos desta função, basta descobrir os pontos críticos de
.Para estudarmos o extremos desta função, basta descobrir os pontos críticos de 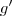 e analisa-os .
e analisa-os . .
. .
. não podemos afirmar nada ,entretanto quando
não podemos afirmar nada ,entretanto quando 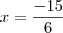 g tem um ponto de mínimo (neste caso global veja a figura abaixo em anexo ) pois ,
g tem um ponto de mínimo (neste caso global veja a figura abaixo em anexo ) pois ,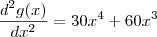 e portanto
e portanto 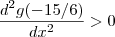 o que significa que há um ponto de mínimo .
o que significa que há um ponto de mínimo .