Mostre que
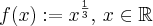, não é diferenciável em 
.Bom, sei que se os limites laterais forem diferentes a função não é diferenciável. Mas os limites laterais em questão são iguais. Como prosseguir?
Obs.: Encontrei os limites pela direita e pela esquerda:
![\lim_{h\rightarrow{0}^{+}}\frac{\sqrt[3]{{(a+h)}^{2}}-\sqrt[3]{{(a)}^{2}}}{h(\sqrt[3]{(a+h)}+\sqrt[3]{a})}](/latexrender/pictures/ed008f8b430a66900bc2543860199715.png "\lim_{h\rightarrow{0}^{+}}\frac{\sqrt[3]{{(a+h)}^{2}}-\sqrt[3]{{(a)}^{2}}}{h(\sqrt[3]{(a+h)}+\sqrt[3]{a})}")
e pela esquerda ![\lim_{h\rightarrow{0}^{-}}\frac{\sqrt[3]{{(a+h)}^{2}}-\sqrt[3]{{(a)}^{2}}}{h(\sqrt[3]{(a+h)}+\sqrt[3]{a})}](/latexrender/pictures/c25ae20232c4d5fb8cc1f9b98deb8644.png "\lim_{h\rightarrow{0}^{-}}\frac{\sqrt[3]{{(a+h)}^{2}}-\sqrt[3]{{(a)}^{2}}}{h(\sqrt[3]{(a+h)}+\sqrt[3]{a})}")
Como prosseguir nesse caso em que os limites laterais são iguais?
Ficarei grato se alguém puder me ajudar.
Cleyson007
![f'(x)=\lim_{h \to 0} \space \frac{\sqrt[3]{x+h}-\sqrt[3]{x}}{h}](/latexrender/pictures/b835fdbf067d311aa0f94cb6f7a77296.png "f'(x)=\lim_{h \to 0} \space \frac{\sqrt[3]{x+h}-\sqrt[3]{x}}{h}")
![\sqrt[3]{(x+h)^2}+\sqrt[3]{x+h} \cdot \sqrt[3]{x}+\sqrt[3]{x^2}](/latexrender/pictures/5647619fe9cd7bdcba4255fbe0ffb38e.png "\sqrt[3]{(x+h)^2}+\sqrt[3]{x+h} \cdot \sqrt[3]{x}+\sqrt[3]{x^2}")
![f'(x)=\lim_{h \to 0} \space \frac{x+h-x}{h \cdot \left (\sqrt[3]{(x+h)^2}+\sqrt[3]{x+h} \cdot \sqrt[3]{x}+\sqrt[3]{x^2}}\right)](/latexrender/pictures/30d4d786d56c9e5470f58c780a046988.png "f'(x)=\lim_{h \to 0} \space \frac{x+h-x}{h \cdot \left (\sqrt[3]{(x+h)^2}+\sqrt[3]{x+h} \cdot \sqrt[3]{x}+\sqrt[3]{x^2}}\right)")
