







deosdete escreveu:Seguinte, todos os exemplos de calculo de area usando integral, usa-se uma linha totalmente torta no grafico, demonstrando que integrando, eu posso medir a area de uma figura calquer mesmo que nao seja reta. Mas vou precisar da lei da funçao que gera essa linha torta no grafico. Supondo então que tenho apenas o dominio e a imagem da função, como chego a lei da função para poder aplicar a integral e calcular a area. Se for uma função do primeiro grau é facil ax + b, uma do segundo também ax2+bx+c, mas e se a linha é toda torta é o que? Como chego na lei dela?
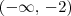 ou
ou  a aproximação não é boa. Isso significa que se o objetivo for calcular a integral no intervalo [-2, 2], então podemos usar a função aproximada para obter o resultado. Mas se o intervalo de integração for fora de [-2, 2], então temos que melhorar de alguma forma a nossa aproximação da função.
a aproximação não é boa. Isso significa que se o objetivo for calcular a integral no intervalo [-2, 2], então podemos usar a função aproximada para obter o resultado. Mas se o intervalo de integração for fora de [-2, 2], então temos que melhorar de alguma forma a nossa aproximação da função.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)