.Qual a velocidade da luz do farol na região costeira quando o ângulo entre o feixe de luz e a perpendicular do farol à praia é de
 (resposta 300 pi m/min) ?
(resposta 300 pi m/min) ?Tentativa de solução :
primeiramente ,considerei um ponto (P) no espaço de modo que sua distância a costa seja ortogonal e equivale 1000 m.
A parti de P a luz se propaga de modo retilineo em sentido a região costeira cujo o Ângulo de incidência é igual a pi/4 .
com essas ideias ,utilizei Pitágoras no Triângulo retângulo e derivei cada parcela em relação ao tempo e achei uma resposta que difere do gabarito .
Alguém poderia sugerir alguma ideia p/ resolver este exercício ?
Obrigado.


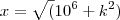

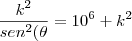


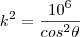
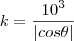
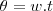 e
e  , logo,
, logo, 
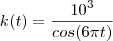

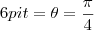
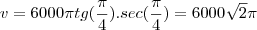 m/min
m/min
![\theta = 6\pi t = \frac{\pi}{4}\\ y=1000 m .\\
10^6 +y^2= z^2 \\
(sin(\theta))^{-2} y^2=z^2 \rightarrow 10^6=y^2([sin(\theta)]^{-2} -1)\\
\frac {d}{dt} y =10^3 6\pi tan(\theta)(1+[tan(\theta)]^2) = 12\pi 10^3 m/min \theta = 6\pi t = \frac{\pi}{4}\\ y=1000 m .\\
10^6 +y^2= z^2 \\
(sin(\theta))^{-2} y^2=z^2 \rightarrow 10^6=y^2([sin(\theta)]^{-2} -1)\\
\frac {d}{dt} y =10^3 6\pi tan(\theta)(1+[tan(\theta)]^2) = 12\pi 10^3 m/min](/latexrender/pictures/6bec866b50b5eaa2552bba52c475dcc5.png)
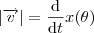 .
. é dado por
é dado por .
. .
.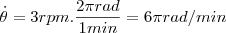 , temos para
, temos para 
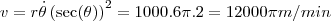 .
. em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.