 por emsbp » Sáb Abr 28, 2012 18:20
por emsbp » Sáb Abr 28, 2012 18:20
Boa tarde.
Peço ajuda no seguinte exercício:
calcule pela definição a derivada da função 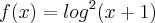
.
Fiz do seguinte modo:
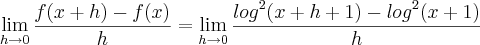
=
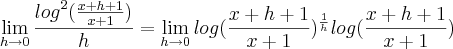
.
A partir daqui, tenho que usar o método por substituição, ou não?
Obrigado!
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
 por LuizAquino » Dom Abr 29, 2012 20:34
por LuizAquino » Dom Abr 29, 2012 20:34
emsbp escreveu:Boa tarde.
Peço ajuda no seguinte exercício:
calcule pela definição a derivada da função 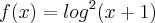
.
Fiz do seguinte modo:
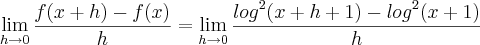
=
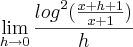
O último passo está errado. O correto seria fazer:
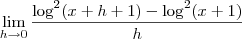
![\,= \lim_{h\to 0}\frac{\left[\log(x+h+1) - \log(x+1)\right]\left[\log(x+h+1) + \log(x+1)\right]}{h} \,= \lim_{h\to 0}\frac{\left[\log(x+h+1) - \log(x+1)\right]\left[\log(x+h+1) + \log(x+1)\right]}{h}](/latexrender/pictures/00ee9e8da62e318f5bc48939664e4c05.png)
![= \lim_{h\to 0}\frac{\left[\log\left(\frac{x+h+1}{x+1}\right)\right]\left\{\log[(x+h+1)(x+1)]\right\}}{h} = \lim_{h\to 0}\frac{\left[\log\left(\frac{x+h+1}{x+1}\right)\right]\left\{\log[(x+h+1)(x+1)]\right\}}{h}](/latexrender/pictures/26cc98aad7c60b1b9cd23b6220fd64ed.png)
![= \left[\lim_{h\to 0}\frac{1}{h}\log\left(1 + \frac{h}{x+1}\right)\right]\lim_{h\to 0} \log[(x+h+1)(x+1)] = \left[\lim_{h\to 0}\frac{1}{h}\log\left(1 + \frac{h}{x+1}\right)\right]\lim_{h\to 0} \log[(x+h+1)(x+1)]](/latexrender/pictures/6c35506710b7e3f39748bb603208cfc6.png)
Agora tente continuar a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por emsbp » Seg Abr 30, 2012 17:29
por emsbp » Seg Abr 30, 2012 17:29
Então, não se pode aplicar as regras dos logaritmos, quando estão em potência?
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
 por LuizAquino » Ter Mai 01, 2012 14:20
por LuizAquino » Ter Mai 01, 2012 14:20
emsbp escreveu:Então, não se pode aplicar as regras dos logaritmos, quando estão em potência?
Naquele caso em questão, não pode.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por emsbp » Qua Mai 02, 2012 06:41
por emsbp » Qua Mai 02, 2012 06:41
Ok. Muito obrigado!
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LIMITES] Limite através da definição
por Henrique Bueno » Sex Abr 19, 2013 00:25
- 1 Respostas
- 1417 Exibições
- Última mensagem por e8group

Sex Abr 19, 2013 02:00
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo de derivada pela definição
por emsbp » Qua Mai 02, 2012 10:34
- 4 Respostas
- 2307 Exibições
- Última mensagem por emsbp

Qua Mai 02, 2012 18:11
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] duas variáveis. Prova através da definição formal
por marcosmuscul » Sáb Jan 25, 2014 17:59
- 2 Respostas
- 6100 Exibições
- Última mensagem por marcosmuscul

Ter Fev 04, 2014 10:03
Cálculo: Limites, Derivadas e Integrais
-
- Derivada através de Ponto Máximo - Otimização
por Suriano » Qua Mai 06, 2009 20:42
- 3 Respostas
- 6214 Exibições
- Última mensagem por Suriano

Qua Mai 13, 2009 21:39
Cálculo
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10878 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
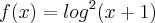 .
.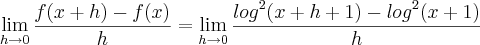 =
= 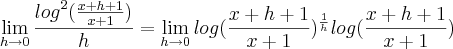 .
.
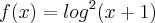 .
.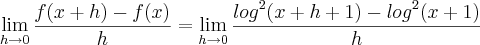 =
= 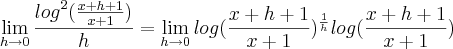 .
.
.
=
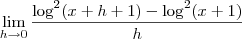
![\,= \lim_{h\to 0}\frac{\left[\log(x+h+1) - \log(x+1)\right]\left[\log(x+h+1) + \log(x+1)\right]}{h} \,= \lim_{h\to 0}\frac{\left[\log(x+h+1) - \log(x+1)\right]\left[\log(x+h+1) + \log(x+1)\right]}{h}](/latexrender/pictures/00ee9e8da62e318f5bc48939664e4c05.png)
![= \lim_{h\to 0}\frac{\left[\log\left(\frac{x+h+1}{x+1}\right)\right]\left\{\log[(x+h+1)(x+1)]\right\}}{h} = \lim_{h\to 0}\frac{\left[\log\left(\frac{x+h+1}{x+1}\right)\right]\left\{\log[(x+h+1)(x+1)]\right\}}{h}](/latexrender/pictures/26cc98aad7c60b1b9cd23b6220fd64ed.png)
![= \left[\lim_{h\to 0}\frac{1}{h}\log\left(1 + \frac{h}{x+1}\right)\right]\lim_{h\to 0} \log[(x+h+1)(x+1)] = \left[\lim_{h\to 0}\frac{1}{h}\log\left(1 + \frac{h}{x+1}\right)\right]\lim_{h\to 0} \log[(x+h+1)(x+1)]](/latexrender/pictures/6c35506710b7e3f39748bb603208cfc6.png)





 .
.



