 por marciommuniz » Qui Jun 11, 2009 00:54
por marciommuniz » Qui Jun 11, 2009 00:54
Olá amigos do site..
estive esses dias discutindo num topico do orkut sobre a integral:
?ln |3x - 2| dx
Lá eles estavam falando que não era integrável, mas não me deram explicações do porquê.
Bem, ao meu ver eu fiz essa integral assim:
?ln|3x-2|dx
INTEGRAÇÃO POR PARTES
u = ln 3x -2
du = (ln 3x-2)' --> REGRA DA CADEIA du = 3/(3x-2)dx
dv = 1. dx --> v = x
?ln |3x-2|dx = uv - ?vdu = ln |3x-2|.x - ?3/(3x-2)dx
vamos agora fazer a integral em negrito
?3/(3x-2)dx
u = 3x -2 du = 3 dx, portando dx = 1/3du , então
?(u+2)/u . 1/3du = 1/3?(u+2)/u
= 1/3? u/u + 2/u = ?1 + ?2/3x-2 = x + 2?dx/3x-2
vamos fazer a outra integral em negrito
u = 3x-2 du = 3dx logo, dx = 1/3du
?dx/3x-2 = ?dx/u . 1/3du = 1/3?dx/u = 1/3.ln |3x-2|
Agora a parte enjoada ahhahaha JUNTAR TUDO!
?ln |3x-2|dx = ln |3x-2|.x - x - 2/3.ln|3x-2| + K, sendo K uma constante.
"Nunca penso no futuro, ele chega rápido demais." Albert Einsten
-
marciommuniz
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 08, 2009 20:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Metalúrgica UFF /Química Lic. UENF
- Andamento: cursando
 por Lucio Carvalho » Qui Ago 20, 2009 13:17
por Lucio Carvalho » Qui Ago 20, 2009 13:17
Olá marciommuniz,
Sou novo no site e sei que o teu tópico já tem algum tempo. Talvez até já chegaste ao resultado!
Também considero que seja possível integrar!
Apresento aqui uma sugestão.
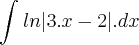
Integrando por partes, ficaria:
u = ln|3.x - 2| => u' = 3/(3.x - 2)
v' = 1 => v = x - 2/3 (Aqui está a novidade!)
Então:
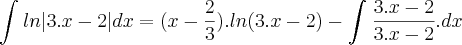
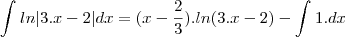
E finalmente, teremos:
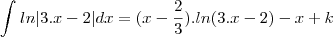
, sendo k = constante.
Penso ser esse um dos resultados. Entretanto, aguardo a opinião dos outros participantes!
-

Lucio Carvalho
- Colaborador Voluntário

-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


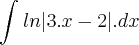
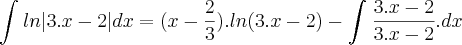
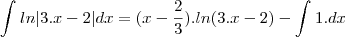
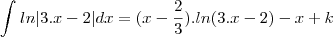 , sendo k = constante.
, sendo k = constante.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.