 por Fabio Wanderley » Ter Mar 27, 2012 14:00
por Fabio Wanderley » Ter Mar 27, 2012 14:00
Muito obrigado, professor! Não conhecia esse artifício matemático (operando com raiz).
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exercício Conjuntos - Meu cálculo está correto?
por sony01 » Seg Abr 23, 2012 16:08
- 3 Respostas
- 14408 Exibições
- Última mensagem por DanielFerreira

Dom Abr 29, 2012 00:50
Álgebra Elementar
-
- [P.A.] Está correto?
por Cleyson007 » Dom Mai 25, 2008 19:37
- 1 Respostas
- 3161 Exibições
- Última mensagem por admin

Dom Mai 25, 2008 19:55
Progressões
-
- [determinante] Está correto?
por Cleyson007 » Sáb Jul 19, 2008 13:21
- 1 Respostas
- 3541 Exibições
- Última mensagem por admin

Sáb Jul 19, 2008 16:40
Matrizes e Determinantes
-
- [Derivada] Esta correto o que eu fiz?
por carvalhothg » Ter Set 13, 2011 13:22
- 2 Respostas
- 1865 Exibições
- Última mensagem por thiago toledo

Ter Set 13, 2011 18:21
Cálculo: Limites, Derivadas e Integrais
-
- Também está correto?
por Cleyson007 » Qui Out 10, 2013 17:27
- 2 Respostas
- 1779 Exibições
- Última mensagem por Cleyson007

Sex Out 11, 2013 15:28
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x \to +\infty}\frac{\sqrt[]{x}+\sqrt[3]{x}}{{x}^{2}+ 3} \lim_{x \to +\infty}\frac{\sqrt[]{x}+\sqrt[3]{x}}{{x}^{2}+ 3}](/latexrender/pictures/6ca1407dde047a47a75a29b1119a8941.png)


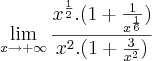

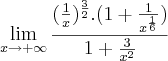


![\lim_{x \to +\infty}\frac{\sqrt[]{x}+\sqrt[3]{x}}{{x}^{2}+ 3} \lim_{x \to +\infty}\frac{\sqrt[]{x}+\sqrt[3]{x}}{{x}^{2}+ 3}](/latexrender/pictures/6ca1407dde047a47a75a29b1119a8941.png)


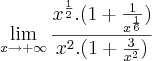

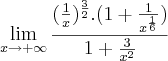


![\lim_{x \to +\infty}\frac{\left(\sqrt{x}+\sqrt[3]{x}\right) : x^2}{\left({x}^{2}+ 3\right):x^2} = \lim_{x \to +\infty}\frac{\sqrt{\frac{x}{x^4}}+\sqrt[3]{\frac{x}{x^6}}}{1 + \frac{3}{x^2}} \lim_{x \to +\infty}\frac{\left(\sqrt{x}+\sqrt[3]{x}\right) : x^2}{\left({x}^{2}+ 3\right):x^2} = \lim_{x \to +\infty}\frac{\sqrt{\frac{x}{x^4}}+\sqrt[3]{\frac{x}{x^6}}}{1 + \frac{3}{x^2}}](/latexrender/pictures/5842115c553261f4c27471b0bae9a7f7.png)
![\lim_{x \to +\infty}\frac{\sqrt{\frac{1}{x^3}}+\sqrt[3]{\frac{1}{x^5}}}{1 + \frac{3}{x^2}} = \frac{\sqrt{0} + \sqrt{0}}{1 + 0} = 0 \lim_{x \to +\infty}\frac{\sqrt{\frac{1}{x^3}}+\sqrt[3]{\frac{1}{x^5}}}{1 + \frac{3}{x^2}} = \frac{\sqrt{0} + \sqrt{0}}{1 + 0} = 0](/latexrender/pictures/1c012f701bcdf431d1da46f01e3381f3.png)



 .
.



