paula luna escreveu:Oi estou com muita dificuldade com esta questao, se alguem conseguir resolve-la por favor poste a resoluçao. Segue abaixo a questao com resposta e tambem o que eu tentei.
Questao:
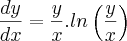
Resposta:
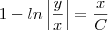
paula luna escreveu:Minha tentativa: Bem, antes de botar as expressoes eu queria tambem perguntar se esta questao tambem nao poderia ser feita por 'variaveis separaveis' diretamente.
Não poderia.
Ok.
paula luna escreveu:Arrumando...
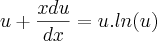
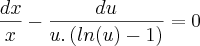
Ok.
paula luna escreveu:Aplicando a integral nos 2 lados:
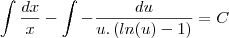
Calculando ...
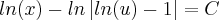
Apenas corrigindo:
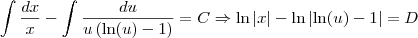 Obs. 1:
Obs. 1: Lembre-se que ao calcular as duas integrais surgirão duas novas constantes, que irão subtrair
C dando origem a uma outra constante
D.
paula luna escreveu:Daqui pra frente eu usei propriedade de log e exponencial pra tranfsrmar a subtraçao de logs em divisao e poder retirar uma das logs ( meio confuso mas acho que da pra intender aqui embaixo)
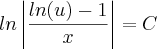
Errado. O correto seria:
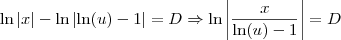
Disso temos que:
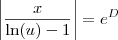
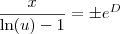
Note que
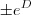
é uma constante. Vamos chamá-la de
E.
Desse modo, temos que:
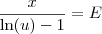
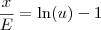
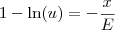
Lembrando que
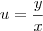
e chamando a constante
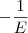
de
F , temos que:
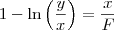 Obs. 2:
Obs. 2: Vale lembrar que o "nome" que damos as constantes não importa. A cada passo você pode chamá-las de tal modo que no fim a resposta fique no formato do gabarito.
Obs. 3: Da forma como foi apresentada a EDO, devemos ter
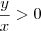
, pois essa expressão está dentro do logaritmo que aparece no segundo membro da equação. Portanto, na resposta final essa expressão não precisa aparecer em módulo.
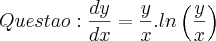
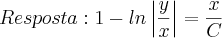
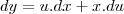
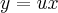
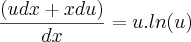
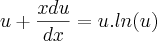
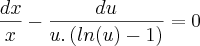
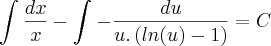
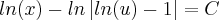
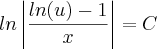
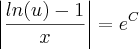
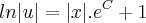
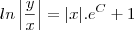
 por quem leu, quem tentou, quem conseguiu ....
por quem leu, quem tentou, quem conseguiu ....


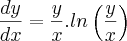
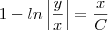
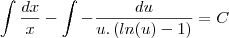
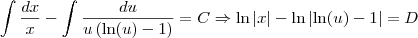
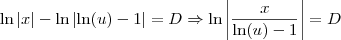
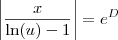
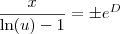
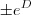 é uma constante. Vamos chamá-la de
é uma constante. Vamos chamá-la de 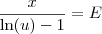
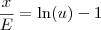
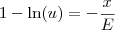
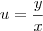 e chamando a constante
e chamando a constante 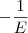 de
de 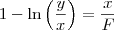
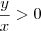 , pois essa expressão está dentro do logaritmo que aparece no segundo membro da equação. Portanto, na resposta final essa expressão não precisa aparecer em módulo.
, pois essa expressão está dentro do logaritmo que aparece no segundo membro da equação. Portanto, na resposta final essa expressão não precisa aparecer em módulo.