 por beel » Dom Nov 27, 2011 20:54
por beel » Dom Nov 27, 2011 20:54
Considere a regiao delimitada pelo grafico da função F(x)=
![\sqrt[]{c^2 -x^2} \sqrt[]{c^2 -x^2}](/latexrender/pictures/b3304603faeb048033782759cc868708.png)
, o eixo Ox e as retas x=-c e x=c, onde c maior que 0.O volume do solido obtido pela rotação em torno do eixo Ox é.
Eu fiz assim,
![\int_{-c}^{c}\Pi(\sqrt[]{c^2 -x^2})^2 dx \int_{-c}^{c}\Pi(\sqrt[]{c^2 -x^2})^2 dx](/latexrender/pictures/b64c4dda60d5d659594a1d6d46224715.png)
ficou:

, aplicados de -c até c
fiquei muito em duvida em como fazer dai em diante
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Seg Nov 28, 2011 16:36
por LuizAquino » Seg Nov 28, 2011 16:36
beel escreveu:Considere a regiao delimitada pelo grafico da função
![F(x)=[tex]\sqrt[]{c^2 -x^2} F(x)=[tex]\sqrt[]{c^2 -x^2}](/latexrender/pictures/c56204722413cd88af7f49561be70ac9.png)
[/tex], o eixo Ox e as retas x=-c e x=c, onde c maior que 0.O volume do solido obtido pela rotação em torno do eixo Ox é.
Eu fiz assim,
![\int_{-c}^{c}\Pi(\sqrt[]{c^2 -x^2})^2 dx \int_{-c}^{c}\Pi(\sqrt[]{c^2 -x^2})^2 dx](/latexrender/pictures/b64c4dda60d5d659594a1d6d46224715.png)
ficou:

, aplicados de -c até c
fiquei muito em duvida em como fazer dai em diante
Para conferir a sua resolução, siga os procedimentos abaixo.
- Acesse a página: http://www.wolframalpha.com/
- No campo de entrada, digite:
- Código: Selecionar todos
integrate pi*(sqrt(c^2 - x^2))^2 dx
- Clique no botão de igual ao lado do campo de entrada.
- Após a integral ser calculada, clique no botão "Show steps" ao lado do resultado.
- Pronto! Agora basta estudar a resolução e comparar com a sua.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Dom Dez 04, 2011 21:14
por beel » Dom Dez 04, 2011 21:14
a integral é definida... o enunciado fala que a função é delimitada pelas retas x=c e x=-c...fiz uma substituição trigonometrica e cai nisso

, mas nao to conseguindo achar uma primitiva...fuuui naquele site mas nao achei nenhuma resultado
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Seg Dez 05, 2011 11:02
por LuizAquino » Seg Dez 05, 2011 11:02
beel escreveu:a integral é definida... o enunciado fala que a função é delimitada pelas retas x=c e x=-c...fiz uma substituição trigonometrica e cai nisso

, mas nao to conseguindo achar uma primitiva...fuuui naquele site mas nao achei nenhuma resultado
Utilizando o procedimento indicado acima, você irá obter o passo a passo do cálculo da integral
indefinida 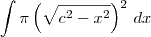
. Ou seja, você poderá verificar o passo a passo de como obter a primitiva de

.
Note que não é necessário utilizar substituição trigonométrica, pois para
![x\in [-c,\, c] x\in [-c,\, c]](/latexrender/pictures/a6b7fb11bcf6827a85be0b88a4ad3c85.png)
temos que
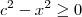
, o que significa que podemos escrever:

Eis a resposta final que será apresentada na página indicada no procedimento:
Indefinite integrals:
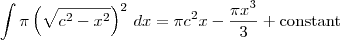
Agora tudo que
você precisa fazer é aplicar o Teorema Fundamental do Cálculo:
![\int_{-c}^{c} \pi\left(\sqrt{c^2 - x^2}\right)^2 dx = \left[\pi c^2 x - \frac{\pi x^3}{3}\right]_{-c}^c \int_{-c}^{c} \pi\left(\sqrt{c^2 - x^2}\right)^2 dx = \left[\pi c^2 x - \frac{\pi x^3}{3}\right]_{-c}^c](/latexrender/pictures/fc257704505b88926deaa1af9daf4109.png)
![=\left[\pi c^2 \cdot c - \frac{\pi \cdot c^3}{3}\right] - \left[\pi c^2\cdot (-c) - \frac{\pi \cdot (-c)^3}{3}\right] =\left[\pi c^2 \cdot c - \frac{\pi \cdot c^3}{3}\right] - \left[\pi c^2\cdot (-c) - \frac{\pi \cdot (-c)^3}{3}\right]](/latexrender/pictures/fca794af4cc81e93c4b7db5f12d0e0ba.png)
![=\left[\pi c^3 - \frac{\pi c^3}{3}\right] - \left[-\pi c^3 + \frac{\pi c^3}{3}\right] =\left[\pi c^3 - \frac{\pi c^3}{3}\right] - \left[-\pi c^3 + \frac{\pi c^3}{3}\right]](/latexrender/pictures/6c1ecf3069941da497ceca7596ae1af6.png)

Por fim, você pode conferir o seu resultado digitando no campo de entrada da página indicada:
- Código: Selecionar todos
integrate pi*(sqrt(c^2 - x^2))^2 dx x=-c..c
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [calculo] volume por integral
por beel » Dom Nov 27, 2011 20:44
- 5 Respostas
- 5054 Exibições
- Última mensagem por LuizAquino

Seg Dez 05, 2011 10:30
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de volume por Integral definida
 por teteffs » Qui Out 06, 2011 17:32
por teteffs » Qui Out 06, 2011 17:32
- 7 Respostas
- 6702 Exibições
- Última mensagem por teteffs

Sáb Out 08, 2011 20:18
Cálculo: Limites, Derivadas e Integrais
-
- calculo area e volume - integral
por bicio29 » Qui Out 20, 2011 08:41
- 3 Respostas
- 4039 Exibições
- Última mensagem por LuizAquino

Qui Out 20, 2011 10:30
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de volume atravé de integral dupla
 por maiquel » Qua Out 13, 2010 12:34
por maiquel » Qua Out 13, 2010 12:34
- 1 Respostas
- 7383 Exibições
- Última mensagem por armando

Sex Jan 06, 2017 04:14
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo do Volume] Variação do volume em porcentagem
por Douglaasag » Sex Out 10, 2014 09:23
- 0 Respostas
- 4475 Exibições
- Última mensagem por Douglaasag

Sex Out 10, 2014 09:23
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{c^2 -x^2} \sqrt[]{c^2 -x^2}](/latexrender/pictures/b3304603faeb048033782759cc868708.png) , o eixo Ox e as retas x=-c e x=c, onde c maior que 0.O volume do solido obtido pela rotação em torno do eixo Ox é.
, o eixo Ox e as retas x=-c e x=c, onde c maior que 0.O volume do solido obtido pela rotação em torno do eixo Ox é.![\int_{-c}^{c}\Pi(\sqrt[]{c^2 -x^2})^2 dx \int_{-c}^{c}\Pi(\sqrt[]{c^2 -x^2})^2 dx](/latexrender/pictures/b64c4dda60d5d659594a1d6d46224715.png)
 , aplicados de -c até c
, aplicados de -c até c
![\sqrt[]{c^2 -x^2} \sqrt[]{c^2 -x^2}](/latexrender/pictures/b3304603faeb048033782759cc868708.png) , o eixo Ox e as retas x=-c e x=c, onde c maior que 0.O volume do solido obtido pela rotação em torno do eixo Ox é.
, o eixo Ox e as retas x=-c e x=c, onde c maior que 0.O volume do solido obtido pela rotação em torno do eixo Ox é.![\int_{-c}^{c}\Pi(\sqrt[]{c^2 -x^2})^2 dx \int_{-c}^{c}\Pi(\sqrt[]{c^2 -x^2})^2 dx](/latexrender/pictures/b64c4dda60d5d659594a1d6d46224715.png)
 , aplicados de -c até c
, aplicados de -c até c
[/tex], o eixo Ox e as retas x=-c e x=c, onde c maior que 0.O volume do solido obtido pela rotação em torno do eixo Ox é.
, aplicados de -c até c

 , mas nao to conseguindo achar uma primitiva...fuuui naquele site mas nao achei nenhuma resultado
, mas nao to conseguindo achar uma primitiva...fuuui naquele site mas nao achei nenhuma resultado
, mas nao to conseguindo achar uma primitiva...fuuui naquele site mas nao achei nenhuma resultado
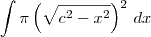 . Ou seja, você poderá verificar o passo a passo de como obter a primitiva de
. Ou seja, você poderá verificar o passo a passo de como obter a primitiva de  .
.![x\in [-c,\, c] x\in [-c,\, c]](/latexrender/pictures/a6b7fb11bcf6827a85be0b88a4ad3c85.png) temos que
temos que 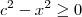 , o que significa que podemos escrever:
, o que significa que podemos escrever:
![\int_{-c}^{c} \pi\left(\sqrt{c^2 - x^2}\right)^2 dx = \left[\pi c^2 x - \frac{\pi x^3}{3}\right]_{-c}^c \int_{-c}^{c} \pi\left(\sqrt{c^2 - x^2}\right)^2 dx = \left[\pi c^2 x - \frac{\pi x^3}{3}\right]_{-c}^c](/latexrender/pictures/fc257704505b88926deaa1af9daf4109.png)
![=\left[\pi c^2 \cdot c - \frac{\pi \cdot c^3}{3}\right] - \left[\pi c^2\cdot (-c) - \frac{\pi \cdot (-c)^3}{3}\right] =\left[\pi c^2 \cdot c - \frac{\pi \cdot c^3}{3}\right] - \left[\pi c^2\cdot (-c) - \frac{\pi \cdot (-c)^3}{3}\right]](/latexrender/pictures/fca794af4cc81e93c4b7db5f12d0e0ba.png)
![=\left[\pi c^3 - \frac{\pi c^3}{3}\right] - \left[-\pi c^3 + \frac{\pi c^3}{3}\right] =\left[\pi c^3 - \frac{\pi c^3}{3}\right] - \left[-\pi c^3 + \frac{\pi c^3}{3}\right]](/latexrender/pictures/6c1ecf3069941da497ceca7596ae1af6.png)

