![\lim_{x\rightarrow\infty}[(e^x + x)]^\frac{2}{x} \lim_{x\rightarrow\infty}[(e^x + x)]^\frac{2}{x}](/latexrender/pictures/25e7f1e60b8fd2aebee835047bebdb98.png)
nesse limite, a função exponencial por ser continua "dá passagem' pro limite?
fiz baseado nisso e meu resultado deu e²

![\lim_{x\rightarrow\infty}[(e^x + x)]^\frac{2}{x} \lim_{x\rightarrow\infty}[(e^x + x)]^\frac{2}{x}](/latexrender/pictures/25e7f1e60b8fd2aebee835047bebdb98.png)

beel escreveu:
nesse limite, a função exponencial por ser continua "dá passagem' pro limite?
fiz baseado nisso e meu resultado deu e²

![\lim_{x\rightarrow\infty}exp[ln( e^x + x)]^\frac{2}{x}=
exp (\lim_{x\rightarrow\infty} [ln(e^x + x)]\frac{2}{x}=
exp (\lim_{x\rightarrow\infty} [ln(e^x + x)\frac{x}{2}=
exp (\lim_{x\rightarrow\infty} (\frac{[ln(e^x + x)]\prime}{(\frac{x}{2}\prime)}=
exp (\lim_{x\rightarrow\infty} \frac{\frac{e^x + 1}{e^x + x}}{\frac{1}{2}})=
exp (\lim_{x\rightarrow\infty}\frac{2(e^x + 1)}{e^x + x})= \lim_{x\rightarrow\infty}exp[ln( e^x + x)]^\frac{2}{x}=
exp (\lim_{x\rightarrow\infty} [ln(e^x + x)]\frac{2}{x}=
exp (\lim_{x\rightarrow\infty} [ln(e^x + x)\frac{x}{2}=
exp (\lim_{x\rightarrow\infty} (\frac{[ln(e^x + x)]\prime}{(\frac{x}{2}\prime)}=
exp (\lim_{x\rightarrow\infty} \frac{\frac{e^x + 1}{e^x + x}}{\frac{1}{2}})=
exp (\lim_{x\rightarrow\infty}\frac{2(e^x + 1)}{e^x + x})=](/latexrender/pictures/bee2d00a85fa7dbcde76094890df19b6.png)


beel escreveu:![\lim_{x\rightarrow\infty}exp[ln( e^x + x)]^\frac{2}{x} = exp (\lim_{x\rightarrow\infty} [ln(e^x + x)]\frac{2}{x} \lim_{x\rightarrow\infty}exp[ln( e^x + x)]^\frac{2}{x} = exp (\lim_{x\rightarrow\infty} [ln(e^x + x)]\frac{2}{x}](/latexrender/pictures/d03a08e15316bbe58c313dee7768ec95.png)
![= exp (\lim_{x\rightarrow\infty} [ln(e^x + x)\frac{x}{2}= exp (\lim_{x\rightarrow\infty} (\frac{[ln(e^x + x)]\prime}{(\frac{x}{2}\prime)} = exp (\lim_{x\rightarrow\infty} [ln(e^x + x)\frac{x}{2}= exp (\lim_{x\rightarrow\infty} (\frac{[ln(e^x + x)]\prime}{(\frac{x}{2}\prime)}](/latexrender/pictures/b4e4d97d5b01ddcd207b0bdc0e71d937.png)
continua...
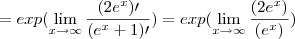
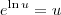 (com u > 0).
(com u > 0). , temos que
, temos que 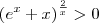 .
. . Sendo assim, podemos escrever:
. Sendo assim, podemos escrever: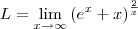

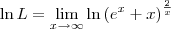
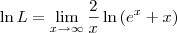
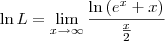
![\ln L = \lim_{x\to\infty} \frac{\left[\ln \left(e^x + x\right)\right]^\prime}{\left(\frac{x}{2}\right)^\prime} \ln L = \lim_{x\to\infty} \frac{\left[\ln \left(e^x + x\right)\right]^\prime}{\left(\frac{x}{2}\right)^\prime}](/latexrender/pictures/d3ba8ca1e543c1a9861e841aebab6d79.png)
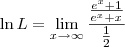
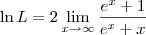

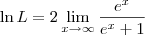

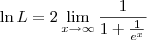
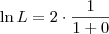


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)