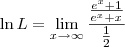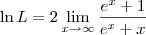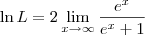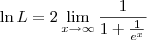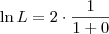por beel » Dom Out 30, 2011 17:51
por beel » Dom Out 30, 2011 17:51
![\lim_{x\rightarrow\infty}[(e^x + x)]^\frac{2}{x} \lim_{x\rightarrow\infty}[(e^x + x)]^\frac{2}{x}](/latexrender/pictures/25e7f1e60b8fd2aebee835047bebdb98.png)
nesse limite, a função exponencial por ser continua "dá passagem' pro limite?
fiz baseado nisso e meu resultado deu e²
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Dom Out 30, 2011 18:24
por LuizAquino » Dom Out 30, 2011 18:24
beel escreveu: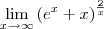
nesse limite, a função exponencial por ser continua "dá passagem' pro limite?
fiz baseado nisso e meu resultado deu e²
O resultado desse limite é esse. Mas envie o seu desenvolvimento para que possamos verificar se ele está correto.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por beel » Dom Out 30, 2011 18:47
por beel » Dom Out 30, 2011 18:47
![\lim_{x\rightarrow\infty}exp[ln( e^x + x)]^\frac{2}{x}=
exp (\lim_{x\rightarrow\infty} [ln(e^x + x)]\frac{2}{x}=
exp (\lim_{x\rightarrow\infty} [ln(e^x + x)\frac{x}{2}=
exp (\lim_{x\rightarrow\infty} (\frac{[ln(e^x + x)]\prime}{(\frac{x}{2}\prime)}=
exp (\lim_{x\rightarrow\infty} \frac{\frac{e^x + 1}{e^x + x}}{\frac{1}{2}})=
exp (\lim_{x\rightarrow\infty}\frac{2(e^x + 1)}{e^x + x})= \lim_{x\rightarrow\infty}exp[ln( e^x + x)]^\frac{2}{x}=
exp (\lim_{x\rightarrow\infty} [ln(e^x + x)]\frac{2}{x}=
exp (\lim_{x\rightarrow\infty} [ln(e^x + x)\frac{x}{2}=
exp (\lim_{x\rightarrow\infty} (\frac{[ln(e^x + x)]\prime}{(\frac{x}{2}\prime)}=
exp (\lim_{x\rightarrow\infty} \frac{\frac{e^x + 1}{e^x + x}}{\frac{1}{2}})=
exp (\lim_{x\rightarrow\infty}\frac{2(e^x + 1)}{e^x + x})=](/latexrender/pictures/bee2d00a85fa7dbcde76094890df19b6.png)
continua...
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por beel » Dom Out 30, 2011 18:58
por beel » Dom Out 30, 2011 18:58
-
beel
- Colaborador Voluntário

-
- Mensagens: 172
- Registrado em: Sex Ago 26, 2011 13:14
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LIMITE]LIMITE FUNDAMENTAL EXPONENCIAL
por beel » Sáb Set 03, 2011 22:11
- 3 Respostas
- 2383 Exibições
- Última mensagem por beel

Dom Set 04, 2011 17:25
Cálculo: Limites, Derivadas e Integrais
-
- Limite com Exponencial
por Thyago Quimica » Qui Mai 24, 2012 17:44
- 1 Respostas
- 1047 Exibições
- Última mensagem por LuizAquino

Qui Mai 24, 2012 22:03
Cálculo: Limites, Derivadas e Integrais
-
- Limite exponencial
por Jhennyfer » Qua Mai 14, 2014 20:07
- 5 Respostas
- 2830 Exibições
- Última mensagem por e8group

Sex Mai 16, 2014 13:09
Cálculo: Limites, Derivadas e Integrais
-
- limite envolvendo exponencial
por renat » Dom Jun 11, 2017 20:37
- 0 Respostas
- 2834 Exibições
- Última mensagem por renat

Dom Jun 11, 2017 20:37
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] Limite fundamental Exponencial
por antonelli2006 » Ter Set 20, 2011 05:54
- 1 Respostas
- 2030 Exibições
- Última mensagem por LuizAquino

Ter Set 20, 2011 12:22
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow\infty}[(e^x + x)]^\frac{2}{x} \lim_{x\rightarrow\infty}[(e^x + x)]^\frac{2}{x}](/latexrender/pictures/25e7f1e60b8fd2aebee835047bebdb98.png)

![\lim_{x\rightarrow\infty}[(e^x + x)]^\frac{2}{x} \lim_{x\rightarrow\infty}[(e^x + x)]^\frac{2}{x}](/latexrender/pictures/25e7f1e60b8fd2aebee835047bebdb98.png)


![\lim_{x\rightarrow\infty}exp[ln( e^x + x)]^\frac{2}{x}=
exp (\lim_{x\rightarrow\infty} [ln(e^x + x)]\frac{2}{x}=
exp (\lim_{x\rightarrow\infty} [ln(e^x + x)\frac{x}{2}=
exp (\lim_{x\rightarrow\infty} (\frac{[ln(e^x + x)]\prime}{(\frac{x}{2}\prime)}=
exp (\lim_{x\rightarrow\infty} \frac{\frac{e^x + 1}{e^x + x}}{\frac{1}{2}})=
exp (\lim_{x\rightarrow\infty}\frac{2(e^x + 1)}{e^x + x})= \lim_{x\rightarrow\infty}exp[ln( e^x + x)]^\frac{2}{x}=
exp (\lim_{x\rightarrow\infty} [ln(e^x + x)]\frac{2}{x}=
exp (\lim_{x\rightarrow\infty} [ln(e^x + x)\frac{x}{2}=
exp (\lim_{x\rightarrow\infty} (\frac{[ln(e^x + x)]\prime}{(\frac{x}{2}\prime)}=
exp (\lim_{x\rightarrow\infty} \frac{\frac{e^x + 1}{e^x + x}}{\frac{1}{2}})=
exp (\lim_{x\rightarrow\infty}\frac{2(e^x + 1)}{e^x + x})=](/latexrender/pictures/bee2d00a85fa7dbcde76094890df19b6.png)


![\lim_{x\rightarrow\infty}exp[ln( e^x + x)]^\frac{2}{x} = exp (\lim_{x\rightarrow\infty} [ln(e^x + x)]\frac{2}{x} \lim_{x\rightarrow\infty}exp[ln( e^x + x)]^\frac{2}{x} = exp (\lim_{x\rightarrow\infty} [ln(e^x + x)]\frac{2}{x}](/latexrender/pictures/d03a08e15316bbe58c313dee7768ec95.png)
![= exp (\lim_{x\rightarrow\infty} [ln(e^x + x)\frac{x}{2}= exp (\lim_{x\rightarrow\infty} (\frac{[ln(e^x + x)]\prime}{(\frac{x}{2}\prime)} = exp (\lim_{x\rightarrow\infty} [ln(e^x + x)\frac{x}{2}= exp (\lim_{x\rightarrow\infty} (\frac{[ln(e^x + x)]\prime}{(\frac{x}{2}\prime)}](/latexrender/pictures/b4e4d97d5b01ddcd207b0bdc0e71d937.png)

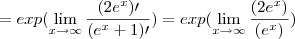
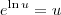 (com u > 0).
(com u > 0). , temos que
, temos que 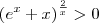 .
. . Sendo assim, podemos escrever:
. Sendo assim, podemos escrever: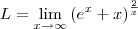

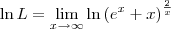
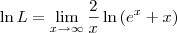
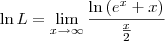
![\ln L = \lim_{x\to\infty} \frac{\left[\ln \left(e^x + x\right)\right]^\prime}{\left(\frac{x}{2}\right)^\prime} \ln L = \lim_{x\to\infty} \frac{\left[\ln \left(e^x + x\right)\right]^\prime}{\left(\frac{x}{2}\right)^\prime}](/latexrender/pictures/d3ba8ca1e543c1a9861e841aebab6d79.png)