Sou novo no fórum e gostaria que algum me ajudasse a encontrar a solução de uma equação diferencial parcial linear de primeira ordem.
Vou começar descrevendo o problema: tenho duas equações diferenciais que descrevem a dinâmica de um trocador de calor solar, porém a que tenho interesse em encontrar a solução é a seguinte:
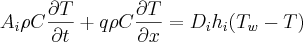
as seguintes variáveis são constantes:
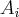 ,
,  ,
,  ,
,  ,
, 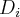 ,
, 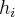 ,
, 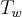 .
.a variação esta em
 .
.Tentei fazer a resolução por um método que encontrei no livro: elements of mathematical ecology, onde se separa a solução em um produto de termos no tempo e espaço:
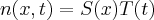 . Neste caso tem-se
. Neste caso tem-se 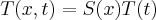 .
.Com isto fiz a substituição na equação original, porém, não consegui arranjar a equação com os termos com derivadas no tempo de um lado e derivadas no espaço no outro, como sugere o autor. Gostaria, se possível, que alguem me ajudasse dando dicas ou até mesmo indicando algum material para eu me basear para encontrar a solução.
att, Gustavo




