PRA RESOLVER UM LIMITE, PRIMEIRO VC TENTA SUBSTITUIR O a em x...MAS SE O DENOMINADOR DER ZERO ( NAO O +/-)TEM QUE FATORAR CERTO?
MAS NESSE CASO, COMO EU RESOLVO?
lim x³+1/x+ 1
x TENDE a -1





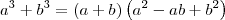
[tex]
\lim_{x\to -1} \frac{x^3 + 1}{x + 1}
[/tex]
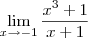



isanobile escreveu:ACHO QUE CONSEGUIR RESOLVER, MEU LIMITE DEU 3
isanobile escreveu:A FORMULA DO POLINOMIO NAO É APENAS QUANDO O X TENDE AO INFINITO?
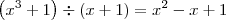
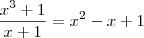


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante