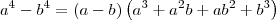por gabrielspadon » Sáb Jul 02, 2011 22:17
por gabrielspadon » Sáb Jul 02, 2011 22:17
Como calculo essas expressões?
![\lim_{x \to \ 3} \frac {\sqrt[3]{x} - \sqrt[3]{3}}{x - 3} \lim_{x \to \ 3} \frac {\sqrt[3]{x} - \sqrt[3]{3}}{x - 3}](/latexrender/pictures/a66a48264a940e9634e60ab7da0a14d2.png)
![\lim_{x \to \ 2} \frac {\sqrt[4]{x} - \sqrt[4]{2}}{x - 2} \lim_{x \to \ 2} \frac {\sqrt[4]{x} - \sqrt[4]{2}}{x - 2}](/latexrender/pictures/527d8ac629ce0c254907486d3200bdc6.png)
Segundo o Guidorrizi vol.1 (Um curso de Calculo), o resultado do primeiro limite é
![\frac {1}{3 \sqrt[3]{9}} \frac {1}{3 \sqrt[3]{9}}](/latexrender/pictures/3d29fabe9ecadee65aa4de36a307d1f4.png)
e o segundo é
![\frac {1}{4 \sqrt[4]{8}} \frac {1}{4 \sqrt[4]{8}}](/latexrender/pictures/062624c0fe5f402c96d2fcac8207f50b.png)
mas não sei como faço para alcançar esses resultados.
-
gabrielspadon
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Jul 02, 2011 22:10
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Sáb Jul 02, 2011 23:10
por MarceloFantini » Sáb Jul 02, 2011 23:10
Você terá que usar produtos notáveis, como no primeiro caso:

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por gabrielspadon » Sáb Jul 02, 2011 23:16
por gabrielspadon » Sáb Jul 02, 2011 23:16
Por que (a²+ab+b²) e não (a²+2ab+b²) = (a+b)²?
-
gabrielspadon
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Jul 02, 2011 22:10
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Fabio Cabral » Dom Jul 03, 2011 02:23
por Fabio Cabral » Dom Jul 03, 2011 02:23
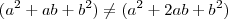
A primeira expressão faz parte da aplicação do produto notável

, como explicado acima.
A segunda expressão faz referência à
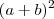
, como você mesmo afirmou:
gabrielspadon escreveu:(a²+2ab+b²) = (a+b)²
Sabendo disso, vamos à sua pergunta.
gabrielspadon escreveu:Por que (a²+ab+b²) e não (a²+2ab+b²) = (a+b)²?
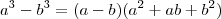
Note que o que há do lado esquerdo da igualdade é equivalente ao lado direito da igualdade, ou seja, resultam na mesma coisa.
Portanto, se resolver o lado direito da igualdade, você obterá

Agora, suponhamos que o lado direito da igualdade seja o que você mencionou:


Se resolver o lado direito da igualdade, o resultado será

?
Não!Por isso você não pode utilizar

ao invés de

Dê uma olhada nesse site. Ele fornece algumas informações úteis sobre produtos notáveis e ainda disponibiliza alguns exercícios!
http://www.exatas.mat.br/produtosnot.htm" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Fabio Cabral » Dom Jul 03, 2011 02:29
por Fabio Cabral » Dom Jul 03, 2011 02:29
viewtopic.php?f=120&t=5302Aqui, uma questão (resolvida) semelhante à essa que você tem dificuldade.
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por gabrielspadon » Dom Jul 03, 2011 11:28
por gabrielspadon » Dom Jul 03, 2011 11:28
Obrigado, consegui calcular e entender o primeiro limite, mas ainda não consegui enxergar qual produto notável se encaixa no segundo limite...
Resolvendo exercícios, notei o seguinte:
![\lim_{x \to \ p} \frac {\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \frac {1}{n \sqrt[n]{p^{n-1}}} \lim_{x \to \ p} \frac {\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \frac {1}{n \sqrt[n]{p^{n-1}}}](/latexrender/pictures/6fc60b8d7b944766d12e09704fed7727.png)
e tambem que:
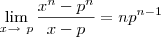
Gostaria de entender o porque disso...
Pois expandindo a primeira equação chego em
![\lim_{x \to \ p} \frac {\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to \ p} \frac {1}{\sqrt[n]{x^{n-1}} - \sqrt[n]{p^{n-1}}} \lim_{x \to \ p} \frac {\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to \ p} \frac {1}{\sqrt[n]{x^{n-1}} - \sqrt[n]{p^{n-1}}}](/latexrender/pictures/c007c7fcdbdc25fae60db78572571946.png)
E não consigo explicar porque o resultado que eu alcancei é equivalente a outro.
-
gabrielspadon
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Jul 02, 2011 22:10
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Renato_RJ » Dom Jul 03, 2011 12:53
por Renato_RJ » Dom Jul 03, 2011 12:53
Em resumo, você acabou de determinar a derivada da função no ponto P..
Se você tem o Guidorizzi recomendo a leitura das páginas 136 até 146, especialmente a página 146 onde tem a demonstração da derivada de
![\sqrt[n]{x} \sqrt[n]{x}](/latexrender/pictures/13fcbed8bcac58d95c0cb989f3aca2de.png)
.
Abraços.
Editado pela última vez por
Renato_RJ em Dom Jul 03, 2011 13:19, em um total de 1 vez.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por gabrielspadon » Dom Jul 03, 2011 13:02
por gabrielspadon » Dom Jul 03, 2011 13:02
Renato_RJ escreveu:Em resumo, você acabou de determinar a derivada da função no ponto P...
Voce poderia me dar uma definição melhor sobre isso? :x
-
gabrielspadon
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Jul 02, 2011 22:10
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Claudin » Dom Jul 03, 2011 14:21
por Claudin » Dom Jul 03, 2011 14:21
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Dom Jul 03, 2011 14:26
por Claudin » Dom Jul 03, 2011 14:26
A resolução destes exercícios no livro é logo no início do estudo sobre Limite, então o aluno seguindo a regra normal de estudo de Cálculo Integral e Diferencial I, ainda não possui conhecimento de derivada, e claro regra de L'Hopital. O modo correto seria aplicação de produtos notáveis como nos tópicos em que eu postei.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Renato_RJ » Dom Jul 03, 2011 14:52
por Renato_RJ » Dom Jul 03, 2011 14:52
Ha, sim, mas esse exercício dá uma introdução ao conceito de derivada, que será visto mais adiante.. Fora que estamos no final do período letivo de qualquer universidade, então o conceito de derivada bem como integral já deveria ser familiar a todos os alunos de Calculo 1...
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Fabio Cabral » Dom Jul 03, 2011 15:35
por Fabio Cabral » Dom Jul 03, 2011 15:35
gabrielspadon escreveu:Obrigado, consegui calcular e entender o primeiro limite, mas ainda não consegui enxergar qual produto notável se encaixa no segundo limite...
Veja que o produto notável a ser usado no segundo limite é:
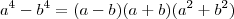
Resolva da mesma maneira do primeiro limite.
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por LuizAquino » Qua Jul 06, 2011 00:22
por LuizAquino » Qua Jul 06, 2011 00:22
DicaEm exercícios como esse lembre-se do produto notável:
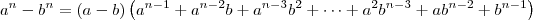
, com n natural e n > 1.
Exemplo:
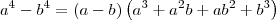
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por giulioaltoe » Qua Jul 06, 2011 00:35
por giulioaltoe » Qua Jul 06, 2011 00:35
tem faculdades que estavam em greve... estou vendo limite so agora!! alias tenhos um exercicio bem semelhante a este dele so que com outras incognitas!
-
giulioaltoe
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Qui Jun 23, 2011 21:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia metalurgica e mat - UENF
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6648 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4793 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5124 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7266 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4444 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x \to \ 3} \frac {\sqrt[3]{x} - \sqrt[3]{3}}{x - 3} \lim_{x \to \ 3} \frac {\sqrt[3]{x} - \sqrt[3]{3}}{x - 3}](/latexrender/pictures/a66a48264a940e9634e60ab7da0a14d2.png)
![\lim_{x \to \ 2} \frac {\sqrt[4]{x} - \sqrt[4]{2}}{x - 2} \lim_{x \to \ 2} \frac {\sqrt[4]{x} - \sqrt[4]{2}}{x - 2}](/latexrender/pictures/527d8ac629ce0c254907486d3200bdc6.png)
![\frac {1}{3 \sqrt[3]{9}} \frac {1}{3 \sqrt[3]{9}}](/latexrender/pictures/3d29fabe9ecadee65aa4de36a307d1f4.png) e o segundo é
e o segundo é ![\frac {1}{4 \sqrt[4]{8}} \frac {1}{4 \sqrt[4]{8}}](/latexrender/pictures/062624c0fe5f402c96d2fcac8207f50b.png) mas não sei como faço para alcançar esses resultados.
mas não sei como faço para alcançar esses resultados.
![\lim_{x \to \ 3} \frac {\sqrt[3]{x} - \sqrt[3]{3}}{x - 3} \lim_{x \to \ 3} \frac {\sqrt[3]{x} - \sqrt[3]{3}}{x - 3}](/latexrender/pictures/a66a48264a940e9634e60ab7da0a14d2.png)
![\lim_{x \to \ 2} \frac {\sqrt[4]{x} - \sqrt[4]{2}}{x - 2} \lim_{x \to \ 2} \frac {\sqrt[4]{x} - \sqrt[4]{2}}{x - 2}](/latexrender/pictures/527d8ac629ce0c254907486d3200bdc6.png)
![\frac {1}{3 \sqrt[3]{9}} \frac {1}{3 \sqrt[3]{9}}](/latexrender/pictures/3d29fabe9ecadee65aa4de36a307d1f4.png) e o segundo é
e o segundo é ![\frac {1}{4 \sqrt[4]{8}} \frac {1}{4 \sqrt[4]{8}}](/latexrender/pictures/062624c0fe5f402c96d2fcac8207f50b.png) mas não sei como faço para alcançar esses resultados.
mas não sei como faço para alcançar esses resultados.


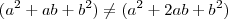
 , como explicado acima.
, como explicado acima.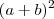 , como você mesmo afirmou:
, como você mesmo afirmou: 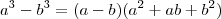



 ?
? ao invés de
ao invés de 


![\lim_{x \to \ p} \frac {\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \frac {1}{n \sqrt[n]{p^{n-1}}} \lim_{x \to \ p} \frac {\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \frac {1}{n \sqrt[n]{p^{n-1}}}](/latexrender/pictures/6fc60b8d7b944766d12e09704fed7727.png)
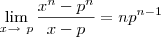
![\lim_{x \to \ p} \frac {\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to \ p} \frac {1}{\sqrt[n]{x^{n-1}} - \sqrt[n]{p^{n-1}}} \lim_{x \to \ p} \frac {\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to \ p} \frac {1}{\sqrt[n]{x^{n-1}} - \sqrt[n]{p^{n-1}}}](/latexrender/pictures/c007c7fcdbdc25fae60db78572571946.png)

![\sqrt[n]{x} \sqrt[n]{x}](/latexrender/pictures/13fcbed8bcac58d95c0cb989f3aca2de.png) .
.




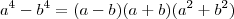

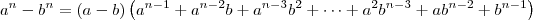 , com n natural e n > 1.
, com n natural e n > 1.