Gostaria que alguém me ajudasse em um probleminha.
Tentei resolve-lo de diversas maneiras mas não deu certo. Vamos ao problema:
-Considere a possibilidade de você estar escalando um morro cujo formato é dado por:
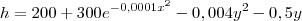
onde o eixo x está orientado para leste e o eixo y para o norte. Se sua posição inicial é
x=100m y=40m e h=248m, em que direção terá a máxima inclinação? Qual a taxa de elevação? Qual o ângulo de elevação de h?
R: u=[-0,937 ; -0,348] ou -159,6º em relação a x
Taxa máxima = 2,35m/m
ângulo = 67º
Gostaria de saber o que eu uso para resolver o problema:
*Derivada direcional? Na direção de qual vetor? Em que ponto?
*Gradiente da função?
Ou outra coisa?
Muito obrigada


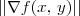 e ele ocorre na direção de
e ele ocorre na direção de  .
.
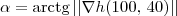
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)