A figura abaixo ilustra o exercício.
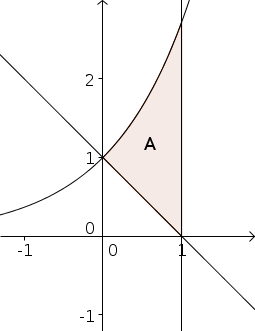
- área-A.png (6.31 KiB) Exibido 2201 vezes
Para determinar a interseção entre
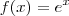
e
g(
x) = 1 -
x, você precisaria resolver a equação
f(
x) =
g(
x), ou seja,
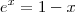
. Acontece que não temos um meio analítico de determinar a solução dessa equação. Porém, não é difícil perceber que
x = 0 é a solução. Ora, como
f(0)=
g(0)=1, temos que o ponto de interseção é (0, 1).
Por outro lado, temos as retas
x = 1 e
g(
x) = 1 -
x. Ora, note que o ponto de interseção necessariamente tem o formato (1, y). Para determinar y, basta calcular y =
g(1) = 0. Portanto, o ponto de interseção é (1, 0).
Por fim, temos a reta
x = 1 e a curva
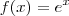
. Ora, note que o ponto de interseção necessariamente tem o formato (1, y). Para determinar y, basta calcular y =
f(1) =
e. Portanto, o ponto de interseção é (1,
e).
Considerando essas informações, temos que:
![A = \int_0^1 e^x - (1 - x)\,dx = \left[e^x - x + \frac{x^2}{2}\right]_0^1 = e - \frac{3}{2} A = \int_0^1 e^x - (1 - x)\,dx = \left[e^x - x + \frac{x^2}{2}\right]_0^1 = e - \frac{3}{2}](/latexrender/pictures/1f651390864cc7f1c3e5c3c97e6093e3.png)
u. a. (unidade de área).


 é uma curva...
é uma curva...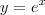 e y = 1 com interseção em x = 0, que será a primeira interseção... a outra interseção será em x=1, que é o outro delimitador da área...
e y = 1 com interseção em x = 0, que será a primeira interseção... a outra interseção será em x=1, que é o outro delimitador da área...![\\
A=\int_0^1[ e^x-1 ]dx\\
A=[ e^x-x ]_0^1\\
A=[ e^1-1 ]-[e^0-0]\\
A=[ e-1 ] - [1]\\
A=e-1-1\\
A=(e-2)u.a. \\
A=\int_0^1[ e^x-1 ]dx\\
A=[ e^x-x ]_0^1\\
A=[ e^1-1 ]-[e^0-0]\\
A=[ e-1 ] - [1]\\
A=e-1-1\\
A=(e-2)u.a.](/latexrender/pictures/d8f5578b02ad9987b4992abbaf54757a.png)

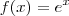 e
e 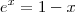 . Acontece que não temos um meio analítico de determinar a solução dessa equação. Porém, não é difícil perceber que
. Acontece que não temos um meio analítico de determinar a solução dessa equação. Porém, não é difícil perceber que ![A = \int_0^1 e^x - (1 - x)\,dx = \left[e^x - x + \frac{x^2}{2}\right]_0^1 = e - \frac{3}{2} A = \int_0^1 e^x - (1 - x)\,dx = \left[e^x - x + \frac{x^2}{2}\right]_0^1 = e - \frac{3}{2}](/latexrender/pictures/1f651390864cc7f1c3e5c3c97e6093e3.png) u. a. (unidade de área).
u. a. (unidade de área).