![\[\lim_{x\to 0+}{\left( \frac{\mathrm{sen}\left( x\right) }{x}\right) }^{x-1}\]](/latexrender/pictures/3ec758ae337ac00465a14558ba9e05de.png "\[\lim_{x\to 0+}{\left( \frac{\mathrm{sen}\left( x\right) }{x}\right) }^{x-1}\]")
Chutei valores perto de 0+, e o limite resultou perto de 1. Será que ta certo? Isso significa que não deu indeterminação ? Não precisa aplicar nenhuma L'Hôpital ?
por Psilocybe » Ter Mai 31, 2011 20:33
por Claudin » Ter Mai 31, 2011 21:20
por carlosalesouza » Qua Jun 01, 2011 00:27
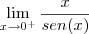, que é um limite notável, igual a 1... logo, o limite lateral existe e é 1Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)