por elbert005 » Ter Mai 31, 2011 15:41
por elbert005 » Ter Mai 31, 2011 15:41
Olá amigos,
Estou com um grande problema para resolução de uma atividade na qual precisarei apresentar amanhã na aula de cálculo.
O problema é o seguinte:
Encontre o ponto P na parábola y=x² que está mais próximo de (3,0) . Justifique sua resposta que o ponto que você encontrou é realmente o mais próximo.
Para resolver eu isolei x e estou trabalhando em termos de y, mais consigo chegar na resposta (1,1). Mas não acho uma maneira de provar essa reposta.
Preciso de ajuda!!!
Elbert
-
elbert005
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Mai 31, 2011 15:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por LuizAquino » Ter Mai 31, 2011 17:23
por LuizAquino » Ter Mai 31, 2011 17:23
Em exercícios de otimização você precisa primeiro obter a função que deseja otimizar. Em boa parte dos exercícios a função não é fornecida diretamente.
Pois bem, perceba que todos os pontos sobre a parábola y = x² têm o formato (k, k²), para algum real k.
Agora, basta armar a função que fornece a distância desse ponto ao ponto (3, 0).
Vale lembrar que dos conhecimentos de Geometria Analítica sabemos que a distância do ponto P = (x0, y0) à Q = (x1, y1) é dada por:

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por elbert005 » Ter Mai 31, 2011 17:48
por elbert005 » Ter Mai 31, 2011 17:48
Boa tarde Luiz,
Eu tenho a seguinte dúvida:
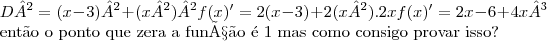
-
elbert005
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Mai 31, 2011 15:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por elbert005 » Ter Mai 31, 2011 17:50
por elbert005 » Ter Mai 31, 2011 17:50
consequentemente a imagem em y= 1² = 1
??????
seria um teste da segunda derivada???
-
elbert005
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Mai 31, 2011 15:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por LuizAquino » Ter Mai 31, 2011 18:08
por LuizAquino » Ter Mai 31, 2011 18:08
D² = (x - 3)² +(x²)²
f'(x) = 2(x-3) + 2(x²).2x
f(x)' = 2x - 6 + 4x³
então o ponto que zera a função é 1 mas como consigo provar isso?
Ora, se você quer comprovar que x = c é raiz da função f(x), então basta você exibir que f(c) = 0. Mas, se você quer explicar como obteve que x = c é uma raiz, aí é outra história. No caso desse exercício, como temos uma equação polinomial, você poderia usar o
Teorema das Raízes Racionais.
Vale lembrar que para concluir que (1, f(1)) é o ponto de mínimo você ainda deve calcular a segunda derivada e verificar se f''(1) > 0.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Otimizacao
por Taisa » Sex Nov 12, 2010 13:53
- 1 Respostas
- 2135 Exibições
- Última mensagem por MarceloFantini

Sex Nov 12, 2010 14:36
Cálculo: Limites, Derivadas e Integrais
-
- Otimização
 por AlbertoAM » Sáb Mai 14, 2011 21:36
por AlbertoAM » Sáb Mai 14, 2011 21:36
- 4 Respostas
- 2475 Exibições
- Última mensagem por AlbertoAM

Dom Mai 15, 2011 19:23
Cálculo: Limites, Derivadas e Integrais
-
- Otimizacao !!!!!!
 por andersoneng » Qua Jun 27, 2012 12:26
por andersoneng » Qua Jun 27, 2012 12:26
- 7 Respostas
- 5253 Exibições
- Última mensagem por andersoneng

Qui Jun 28, 2012 10:24
Cálculo: Limites, Derivadas e Integrais
-
- Otimização
por Jhonata » Seg Fev 25, 2013 19:24
- 1 Respostas
- 1401 Exibições
- Última mensagem por Russman

Seg Fev 25, 2013 20:28
Cálculo: Limites, Derivadas e Integrais
-
- oTIMIZAÇÃO
por Pinheiro Rosa Victor » Qui Mai 02, 2013 11:11
- 0 Respostas
- 1246 Exibições
- Última mensagem por Pinheiro Rosa Victor

Qui Mai 02, 2013 11:11
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 .
.