cada um achou uma resposta diferente.
é uma equação parametrica.


a questao pede a equação da tangente a essa curva no ponto

eu cheguei a seguinte equação :
![y=\frac{\sqrt[]{3}}{2}x + \frac{1}{4} y=\frac{\sqrt[]{3}}{2}x + \frac{1}{4}](/latexrender/pictures/18e7bc902584b47e234971950fb0c057.png)
obrigado




![y=\frac{\sqrt[]{3}}{2}x + \frac{1}{4} y=\frac{\sqrt[]{3}}{2}x + \frac{1}{4}](/latexrender/pictures/18e7bc902584b47e234971950fb0c057.png)

 e queremos a reta tangente em
e queremos a reta tangente em 
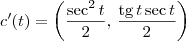 . Para o valor do parâmetro desejado, temos que
. Para o valor do parâmetro desejado, temos que 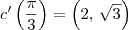 .
.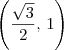 e tem direção dada pelo vetor
e tem direção dada pelo vetor  . Logo, a equação vetorial dessa reta é
. Logo, a equação vetorial dessa reta é 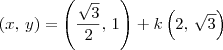 .
.
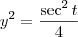
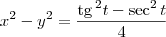
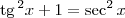 :
:


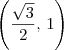 :
: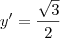


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.