Há duas formas básicas de fazer o exercício.
Você pode trabalhar diretamente com a equação paramétrica ou você pode determinar a equação cartesiana e usar derivação implícita.
Solução 1Usando diretamente a equação paramétrica, temos a curva

e queremos a reta tangente em

Sabemos que a reta tangente terá direção dada por
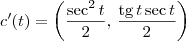
. Para o valor do parâmetro desejado, temos que
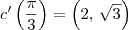
.
Desse modo, a reta tangente passa pelo ponto
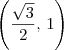
e tem direção dada pelo vetor

. Logo, a equação vetorial dessa reta é
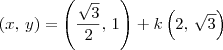
.
Agora, deixo para você o trabalho de passar essa equação da reta para a forma cartesiana.
Solução 2Se você quiser usar a estratégia de transformar a equação paramétrica em equação cartesiana, então basta fazer o que segue abaixo.
Elevando ao quadrado ambos os membros das equações originais:

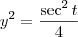
Subtraindo essas equações:
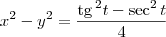
Usando a identidade trigonométrica
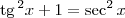
:

Usando derivação implícita:


Lembrando que o ponto desejado é
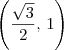
:
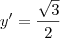
Portanto, a reta tangente será:

Novamente, deixo para você o trabalho de terminar de arrumar a equação da reta.



![y=\frac{\sqrt[]{3}}{2}x + \frac{1}{4} y=\frac{\sqrt[]{3}}{2}x + \frac{1}{4}](/latexrender/pictures/18e7bc902584b47e234971950fb0c057.png)




![y=\frac{\sqrt[]{3}}{2}x + \frac{1}{4} y=\frac{\sqrt[]{3}}{2}x + \frac{1}{4}](/latexrender/pictures/18e7bc902584b47e234971950fb0c057.png)

 e queremos a reta tangente em
e queremos a reta tangente em 
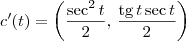 . Para o valor do parâmetro desejado, temos que
. Para o valor do parâmetro desejado, temos que 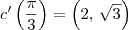 .
.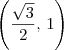 e tem direção dada pelo vetor
e tem direção dada pelo vetor  . Logo, a equação vetorial dessa reta é
. Logo, a equação vetorial dessa reta é 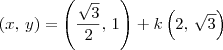 .
.
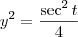
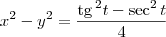
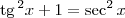 :
:


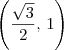 :
: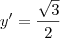



 .
.
 :
: