oi
eu estudo engenharia eletrônica na suécia
to precisando de ajuda
alguem tem nocao como resolver estas questoes? principalmente a 3....
http://apachepersonal.miun.se/~egmpor/S ... nd-in3.pdf
por ratamaria » Sáb Nov 13, 2010 10:35
por luispereira » Qui Dez 23, 2010 22:26
![u(x,t)=\sum^\infty_{n=1}[a_nsin(n\pi)cos(nt)+b_nsin(n\pi)sin(nt)]](/latexrender/pictures/934841cf9c36a6aadc2c281b6ca654d0.png "u(x,t)=\sum^\infty_{n=1}[a_nsin(n\pi)cos(nt)+b_nsin(n\pi)sin(nt)]")
e [/tex] b_n[/tex] são coeficientes da série de Fourier de uma variável. Dado o exercício, o 1ª coeficiente tem duas funções, contínuas, e satisfeitas por:![a_n=\frac{2}{\pi}[\int^\frac{\pi}{2}_0xsin(nx)dx+\int^\pi_\frac{\pi}{2}(\pi-x)sin(nx)dx]](/latexrender/pictures/43041cccf120632ed5bde8a330be64a7.png "a_n=\frac{2}{\pi}[\int^\frac{\pi}{2}_0xsin(nx)dx+\int^\pi_\frac{\pi}{2}(\pi-x)sin(nx)dx]")
![a_n=\frac{4}{n^2\pi}sin(\frac{n\pi}{2})+\frac{2}{n}[(-1)^n-cos(\frac{n\pi}{2})]+\pi](/latexrender/pictures/40a85becc629c737ebcb12a964f531fe.png "a_n=\frac{4}{n^2\pi}sin(\frac{n\pi}{2})+\frac{2}{n}[(-1)^n-cos(\frac{n\pi}{2})]+\pi")
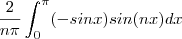. Porém, esta última integral é nula, ou seja: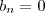 
![u(x,t)=\sum^\infty_{n=1}{[\frac{4}{n^2\pi}sin(\frac{n\pi}{2})+\frac{2}{n}[(-1)^n-cos(\frac{n\pi}{2})]+\pi]sin(n\pi)cos(nt)}](/latexrender/pictures/88c4d34f570ca20785a34d8c325d69c5.png "u(x,t)=\sum^\infty_{n=1}{[\frac{4}{n^2\pi}sin(\frac{n\pi}{2})+\frac{2}{n}[(-1)^n-cos(\frac{n\pi}{2})]+\pi]sin(n\pi)cos(nt)}")
, onde percebe-se que há inúmeras respostas.Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
.
, 
e para 
, 
.
e 
, monte a função e substitua 
por 
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
