 por Adriano Tavares » Qua Mar 09, 2011 00:36
por Adriano Tavares » Qua Mar 09, 2011 00:36
Olá,Loreto.
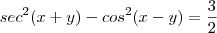
Diferenciando ambos os membros em relação a

teremos:
![2sec(x+y).sec(x+y).tg(x+y).(1+y')-[2cos(x-y).(-sen(x-y).(1-y')]=0 2sec(x+y).sec(x+y).tg(x+y).(1+y')-[2cos(x-y).(-sen(x-y).(1-y')]=0](/latexrender/pictures/e5aa51c5d82d7b4621da77403f8a59f8.png)

Substituindo os valores de

e

teremos:
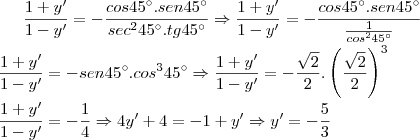
Calculando a reta tangente teremos:
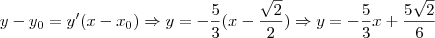
-
Adriano Tavares
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Seg Mar 07, 2011 16:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnólogo em automação industrial
- Andamento: formado
 por Adriano Tavares » Qua Mar 09, 2011 21:56
por Adriano Tavares » Qua Mar 09, 2011 21:56
Olá,LuizAquino.
Creio que não há erro nessa primeira correção,isso porque eu já coloquei o valor direto do resultado da
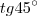
que é igual a

.Note que no meu cálculo aperece o

e no seu apenas o valor do

.Quanto a segunda sim,pois, faltou atenção minha na hora de substituir o valor de

.Eu substitui o valor de

pelo

.
Um abraço!
-
Adriano Tavares
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Seg Mar 07, 2011 16:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnólogo em automação industrial
- Andamento: formado
 por LuizAquino » Qua Mar 09, 2011 22:03
por LuizAquino » Qua Mar 09, 2011 22:03
Olá Adriano Tavares,
Eu atualizei a mensagem removendo essa primeira "correção".
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivação Implicita
por xafabi » Qui Mai 02, 2013 13:56
- 0 Respostas
- 1278 Exibições
- Última mensagem por xafabi

Qui Mai 02, 2013 13:56
Cálculo: Limites, Derivadas e Integrais
-
- Derivação implicita.
por cardoed001 » Sáb Set 28, 2013 21:56
- 2 Respostas
- 2668 Exibições
- Última mensagem por cardoed001

Dom Set 29, 2013 12:28
Cálculo: Limites, Derivadas e Integrais
-
- Derivação Implicita
por victornakaya » Sáb Jun 28, 2014 20:03
- 0 Respostas
- 1178 Exibições
- Última mensagem por victornakaya

Sáb Jun 28, 2014 20:03
Cálculo: Limites, Derivadas e Integrais
-
- Derivação Implicita
por victornakaya » Sáb Jun 28, 2014 20:03
- 1 Respostas
- 1315 Exibições
- Última mensagem por young_jedi

Sáb Jul 05, 2014 16:05
Cálculo: Limites, Derivadas e Integrais
-
- Derivação implicita
por Carolminera » Dom Jul 06, 2014 23:07
- 1 Respostas
- 1309 Exibições
- Última mensagem por young_jedi

Seg Jul 07, 2014 20:07
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





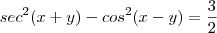
 teremos:
teremos:![2sec(x+y).sec(x+y).tg(x+y).(1+y')-[2cos(x-y).(-sen(x-y).(1-y')]=0 2sec(x+y).sec(x+y).tg(x+y).(1+y')-[2cos(x-y).(-sen(x-y).(1-y')]=0](/latexrender/pictures/e5aa51c5d82d7b4621da77403f8a59f8.png)

 teremos:
teremos: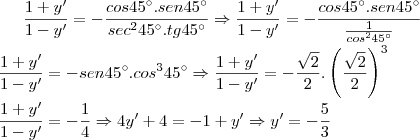
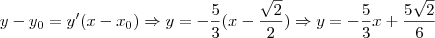




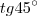 que é igual a
que é igual a  .Note que no meu cálculo aperece o
.Note que no meu cálculo aperece o  e no seu apenas o valor do
e no seu apenas o valor do  .Quanto a segunda sim,pois, faltou atenção minha na hora de substituir o valor de
.Quanto a segunda sim,pois, faltou atenção minha na hora de substituir o valor de  .Eu substitui o valor de
.Eu substitui o valor de  .
. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  .
.
