 por Reh » Qua Jul 20, 2016 18:52
por Reh » Qua Jul 20, 2016 18:52
Problema: Determine o coeficiente angular da curva
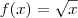
no ponto (4; 2) e a equação
da reta tangente à curva nesse ponto.
Estou com dificuldade em relação a fórmula para calcular, pois quando faço o gráfico e uso dois pontos, por exemplo, p1(4,2) e p2(9,3), para calcular o coeficiente angular
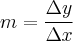
encontro algo que não é o coeficiente angular e da mesma forma para outros pontos do gráfico. Existe uma fórmula para o cálculo?
Desde já, grato pela contribuição.

-
Reh
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Jul 20, 2016 13:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: COMPUTAÇÃO
- Andamento: cursando
 por Daniel Bosi » Qua Jul 20, 2016 21:34
por Daniel Bosi » Qua Jul 20, 2016 21:34
Olá Reh.
Você já aprendeu derivada? A forma de encontrar o coeficiente angular da reta tangente ao ponto da função é fazendo a derivada da função e substituindo o x do ponto (4,2) nessa derivada:
![f(x) = \sqrt[]{x} f(x) = \sqrt[]{x}](/latexrender/pictures/db121f82bd932015c370b06f13645461.png)
Derivada:
![f'(x) = \frac{1}{2\times\sqrt[]{x}} f'(x) = \frac{1}{2\times\sqrt[]{x}}](/latexrender/pictures/ee1613992b11cde7766c340421922857.png)
Substituindo a coordenada x do ponto (4,2) significa substituir o número 4 nessa derivada, encontrando o coeficiente angular da reta tangente

.
Portanto, a equação da reta tangente ao ponto (4,2) da função supracitada deve ser da forma

.
Ainda não conhecemos essa constante c, mas sabemos que a reta passa pelo ponto (4,2). Portanto, para o valor de x igual a 4, o y deve ser 2, assim:

Isso significa que:

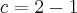

Portanto a equação da reta tangente à função
![f(x) = \sqrt[]{x} f(x) = \sqrt[]{x}](/latexrender/pictures/db121f82bd932015c370b06f13645461.png)
no ponto (4,2) é

-
Daniel Bosi
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Mai 16, 2016 21:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Reh » Qua Jul 20, 2016 23:58
por Reh » Qua Jul 20, 2016 23:58
Resolução perfeita, porém ainda não aprendi derivada. O meu professor disponibilizou essa resolução, sem a aplicação de derivadas, pois a questão é referente a prova de Limites. Detalhe, ele usa uma "fórmula" para encontrar o coeficiente angular.
![m = \lim_{h\rightarrow0} \frac{\sqrt[]{4 + h} - \sqrt[]{4}}{h} = \lim_{h\rightarrow0} \frac{\sqrt[]{4 + h} - \sqrt[]{4}}{h} * {} \frac{\sqrt[]{4 + h} + \sqrt[]{4}}{{\sqrt[]{4+h} + \sqrt[]{4}}{h}} = \lim_{h\rightarrow0} \frac{{4 + h} - {4}}{h\left(\sqrt[]{4+h}+2 \right)} m = \lim_{h\rightarrow0} \frac{\sqrt[]{4 + h} - \sqrt[]{4}}{h} = \lim_{h\rightarrow0} \frac{\sqrt[]{4 + h} - \sqrt[]{4}}{h} * {} \frac{\sqrt[]{4 + h} + \sqrt[]{4}}{{\sqrt[]{4+h} + \sqrt[]{4}}{h}} = \lim_{h\rightarrow0} \frac{{4 + h} - {4}}{h\left(\sqrt[]{4+h}+2 \right)}](/latexrender/pictures/9bb5719d38ff33fbf9b221bed03d5d6a.png)
![= \frac{h}{h\left( \sqrt[]{4+h}+2\right)} = \lim_{h\rightarrow0} \frac{1}{\sqrt[]{4+h}+2} \Rightarrow m = \frac{1}{4} = \frac{h}{h\left( \sqrt[]{4+h}+2\right)} = \lim_{h\rightarrow0} \frac{1}{\sqrt[]{4+h}+2} \Rightarrow m = \frac{1}{4}](/latexrender/pictures/9f5005f922e261d0212029de4624f971.png)
Acredito que a fórmula seja essa
![\lim_{h\rightarrow0} \frac{\sqrt[]{Xo+h}-\sqrt[]{Xo}}{h} \lim_{h\rightarrow0} \frac{\sqrt[]{Xo+h}-\sqrt[]{Xo}}{h}](/latexrender/pictures/441cc3ad2f73807653a47b604dc390bb.png)
aplicado ao ponto (4,2) onde Xo seria o 4, assim sendo substituído na fórmula para calcular o coeficiente angular. Faz sentido?

Excelente dica, obrigado.
-
Reh
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Jul 20, 2016 13:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: COMPUTAÇÃO
- Andamento: cursando
 por Daniel Bosi » Qui Jul 21, 2016 09:23
por Daniel Bosi » Qui Jul 21, 2016 09:23
Bom dia, Reh.
Parece que o seu professor está trabalhando com a Derivada por Limite. Dê uma olhada no link abaixo onde é mostrada a fórmula da Derivada por Limite com exercícios resolvidos:
http://www.mtm.ufsc.br/~azeredo/calculo ... efDer.html
-
Daniel Bosi
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Mai 16, 2016 21:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Reh » Sex Jul 22, 2016 08:58
por Reh » Sex Jul 22, 2016 08:58
Sim, realmente parece ser isso, ótimo site com conteúdos de cálculo, ajudou muito.
Obrigado!

-
Reh
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Jul 20, 2016 13:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: COMPUTAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Coeficiente angular da tangente] Duvidas no resultado
por fabriel » Dom Mai 05, 2013 15:52
- 1 Respostas
- 1415 Exibições
- Última mensagem por young_jedi

Dom Mai 05, 2013 19:24
Cálculo: Limites, Derivadas e Integrais
-
- [drv implícita]coeficiente angular da reta normal ao gráfico
por marcosmuscul » Qui Abr 04, 2013 14:54
- 2 Respostas
- 1789 Exibições
- Última mensagem por marcosmuscul

Qui Abr 04, 2013 17:40
Cálculo: Limites, Derivadas e Integrais
-
- coeficiente angular
por alexsandrob13 » Seg Mai 16, 2011 22:02
- 1 Respostas
- 1931 Exibições
- Última mensagem por Molina

Seg Mai 16, 2011 22:32
Geometria Analítica
-
- Coeficiente angular
por alexsandrob13 » Seg Mai 16, 2011 22:06
- 6 Respostas
- 4477 Exibições
- Última mensagem por alexsandrob13

Ter Mai 17, 2011 20:05
Geometria Analítica
-
- Coeficiente Angular e Taxa de Variação
por Fabio Cabral » Qua Jun 29, 2011 11:43
- 1 Respostas
- 1945 Exibições
- Última mensagem por Claudin

Qua Jun 29, 2011 11:52
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
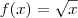 no ponto (4; 2) e a equação
no ponto (4; 2) e a equação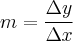 encontro algo que não é o coeficiente angular e da mesma forma para outros pontos do gráfico. Existe uma fórmula para o cálculo?
encontro algo que não é o coeficiente angular e da mesma forma para outros pontos do gráfico. Existe uma fórmula para o cálculo?


![f(x) = \sqrt[]{x} f(x) = \sqrt[]{x}](/latexrender/pictures/db121f82bd932015c370b06f13645461.png)
![f'(x) = \frac{1}{2\times\sqrt[]{x}} f'(x) = \frac{1}{2\times\sqrt[]{x}}](/latexrender/pictures/ee1613992b11cde7766c340421922857.png)
 .
. .
.

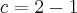



![m = \lim_{h\rightarrow0} \frac{\sqrt[]{4 + h} - \sqrt[]{4}}{h} = \lim_{h\rightarrow0} \frac{\sqrt[]{4 + h} - \sqrt[]{4}}{h} * {} \frac{\sqrt[]{4 + h} + \sqrt[]{4}}{{\sqrt[]{4+h} + \sqrt[]{4}}{h}} = \lim_{h\rightarrow0} \frac{{4 + h} - {4}}{h\left(\sqrt[]{4+h}+2 \right)} m = \lim_{h\rightarrow0} \frac{\sqrt[]{4 + h} - \sqrt[]{4}}{h} = \lim_{h\rightarrow0} \frac{\sqrt[]{4 + h} - \sqrt[]{4}}{h} * {} \frac{\sqrt[]{4 + h} + \sqrt[]{4}}{{\sqrt[]{4+h} + \sqrt[]{4}}{h}} = \lim_{h\rightarrow0} \frac{{4 + h} - {4}}{h\left(\sqrt[]{4+h}+2 \right)}](/latexrender/pictures/9bb5719d38ff33fbf9b221bed03d5d6a.png)
![= \frac{h}{h\left( \sqrt[]{4+h}+2\right)} = \lim_{h\rightarrow0} \frac{1}{\sqrt[]{4+h}+2} \Rightarrow m = \frac{1}{4} = \frac{h}{h\left( \sqrt[]{4+h}+2\right)} = \lim_{h\rightarrow0} \frac{1}{\sqrt[]{4+h}+2} \Rightarrow m = \frac{1}{4}](/latexrender/pictures/9f5005f922e261d0212029de4624f971.png)
![\lim_{h\rightarrow0} \frac{\sqrt[]{Xo+h}-\sqrt[]{Xo}}{h} \lim_{h\rightarrow0} \frac{\sqrt[]{Xo+h}-\sqrt[]{Xo}}{h}](/latexrender/pictures/441cc3ad2f73807653a47b604dc390bb.png) aplicado ao ponto (4,2) onde Xo seria o 4, assim sendo substituído na fórmula para calcular o coeficiente angular. Faz sentido?
aplicado ao ponto (4,2) onde Xo seria o 4, assim sendo substituído na fórmula para calcular o coeficiente angular. Faz sentido? 
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.