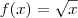 no ponto (4; 2) e a equação
no ponto (4; 2) e a equaçãoda reta tangente à curva nesse ponto.
Estou com dificuldade em relação a fórmula para calcular, pois quando faço o gráfico e uso dois pontos, por exemplo, p1(4,2) e p2(9,3), para calcular o coeficiente angular
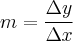 encontro algo que não é o coeficiente angular e da mesma forma para outros pontos do gráfico. Existe uma fórmula para o cálculo?
encontro algo que não é o coeficiente angular e da mesma forma para outros pontos do gráfico. Existe uma fórmula para o cálculo?Desde já, grato pela contribuição.



![f(x) = \sqrt[]{x} f(x) = \sqrt[]{x}](/latexrender/pictures/db121f82bd932015c370b06f13645461.png)
![f'(x) = \frac{1}{2\times\sqrt[]{x}} f'(x) = \frac{1}{2\times\sqrt[]{x}}](/latexrender/pictures/ee1613992b11cde7766c340421922857.png)
 .
. .
.

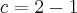



![m = \lim_{h\rightarrow0} \frac{\sqrt[]{4 + h} - \sqrt[]{4}}{h} = \lim_{h\rightarrow0} \frac{\sqrt[]{4 + h} - \sqrt[]{4}}{h} * {} \frac{\sqrt[]{4 + h} + \sqrt[]{4}}{{\sqrt[]{4+h} + \sqrt[]{4}}{h}} = \lim_{h\rightarrow0} \frac{{4 + h} - {4}}{h\left(\sqrt[]{4+h}+2 \right)} m = \lim_{h\rightarrow0} \frac{\sqrt[]{4 + h} - \sqrt[]{4}}{h} = \lim_{h\rightarrow0} \frac{\sqrt[]{4 + h} - \sqrt[]{4}}{h} * {} \frac{\sqrt[]{4 + h} + \sqrt[]{4}}{{\sqrt[]{4+h} + \sqrt[]{4}}{h}} = \lim_{h\rightarrow0} \frac{{4 + h} - {4}}{h\left(\sqrt[]{4+h}+2 \right)}](/latexrender/pictures/9bb5719d38ff33fbf9b221bed03d5d6a.png)
![= \frac{h}{h\left( \sqrt[]{4+h}+2\right)} = \lim_{h\rightarrow0} \frac{1}{\sqrt[]{4+h}+2} \Rightarrow m = \frac{1}{4} = \frac{h}{h\left( \sqrt[]{4+h}+2\right)} = \lim_{h\rightarrow0} \frac{1}{\sqrt[]{4+h}+2} \Rightarrow m = \frac{1}{4}](/latexrender/pictures/9f5005f922e261d0212029de4624f971.png)
![\lim_{h\rightarrow0} \frac{\sqrt[]{Xo+h}-\sqrt[]{Xo}}{h} \lim_{h\rightarrow0} \frac{\sqrt[]{Xo+h}-\sqrt[]{Xo}}{h}](/latexrender/pictures/441cc3ad2f73807653a47b604dc390bb.png) aplicado ao ponto (4,2) onde Xo seria o 4, assim sendo substituído na fórmula para calcular o coeficiente angular. Faz sentido?
aplicado ao ponto (4,2) onde Xo seria o 4, assim sendo substituído na fórmula para calcular o coeficiente angular. Faz sentido? 
