[Derivada] Parcial como Taxa de Variação

por **Whitesttax** » Ter Abr 26, 2016 17:18

Boa tarde.
Não estou conseguindo resolver o seguinte problema:
Um reservatório de areia tem o formato de uma pirâmide invertida de base quadrada. A taxa de vazão da areia deste reservatório diminui a uma velocidade de 40pi cm^3/min.
Esta areia forma no chão um monte cônico. O volume total de areia no reservatório era 243pi cm^3. Determine a velocidade com que aumenta a altura do cone quando um terço da areia já caiu do reservatório. Sabendo que neste instante a altura do monte é 3cm e o raio aumenta uma taxa de 0,3cm/min.

O que já tentei fazer foi aplicar a fórmula do volume do cone, que se estou certo é V = pi*r^2*h / 3. Aí derivei para descobrir a altura mas está dando um resultado negativo, e bem errado (a resposta certa é 1.28cm/min)
Um ponto que talvez errei foi usar a taxa de variação do volume da pirâmide na conta debaixo sem mudar nada, não sei o que teria que mudar... O raio eu consegui aplicando a fórmula do volume também, só que sem derivar.
Mais ou menos assim...
$-40\pi = 2\pi*r*h/3 *0,3 + \pi*r^2/3 * \partial h/\partial t$

Obrigado!

por **adauto martins** » Sáb Mai 07, 2016 21:21

encontrei um valor prox. ao valor da resposta,vamos á soluçao:
1) ${V}_{c}/{V}_{p}=((1/3)\pi.{r}^{2}.{h}_{c})/((1/3).{l}^{2}.{h}_{p})=(\pi.{r}^{2}.{h}_{c})/({l}^{2}.{h}_{p})=1$ ,pois os volumes serao os mesmos...
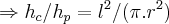
$\Rightarrow {h}_{c}/{h}_{p}={l}^{2}/(\pi.{r}^{2})$ $\Rightarrow {h}_{c}={h}_{p}.{l}^{2}/(\pi.{r}^{2})$ ...
2) ${V}_{p}=(1/3).{l}^{2}.{h}_{p}\Rightarrow (243.3.\pi)={l}^{2}.{h}_{p}\Rightarrow {l}^{2}.{h}_{p}=729.\pi$ ...
substituindo o resultado na prim.relaçao teremos:
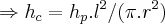${h}_{p}=(729.\pi)/(\pi.{r}^{2})\Rightarrow r=\sqrt[]{729/3}=\sqrt[]{243}\Rightarrow {h'}_{p}=-(729.\pi).2.r.r'/({r}^{4})=-(729.\pi.2).r'/{r}^{3}=-(1458.\pi)/{(\sqrt[]{243)}}^{3})$ ... ${h'}_{p} \simeq -1.21 (cm/mit)$ ,osinal negativo é pq a areia esta caindo,questao de referencial...em valor absoluto é o calculado...

por **adauto martins** » Dom Mai 08, 2016 00:15

caro Whitesttax e colegas do site,
a resoluçao apresentada por mim do exercicio esta incorreta,pois nao levei em consideraçao a açao da gravidade sobre a areia q. cai da piramide...entao em ocasiao oportuna irei apresenta uma soluçao correta,no mais obrigado...

por **adauto martins** » Qua Mai 11, 2016 12:21

vamos considerar a areia q. escoa fazendo o cone,dessa forma podemos eliminar o fator da gravidade q. atua na areia da piramide,entao:
a vazao da areia da piramide sera a mesma q. forma o cone,pois o tempo de esoamento da areia da piramide,sera o mesmo da formaçao do cone,logo:
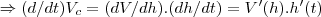$(d/dt){V}_{p}=(d/dt){V}_{c}$ $\Rightarrow (d/dt){V}_{c}=(dV/dh).(dh/dt)=V'(h).h'(t)$ (aqui regra da cadeia)1) 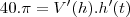$40.\pi=V'(h).h'(t)$ ...temos q.:
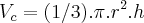${V}_{c}=(1/3).\pi.{r}^{2}.h$ ,p/ o instante pedido teremos:
$(243.\pi)/3=(1/3).\pi.{r}^{2}.h\Rightarrow r=\sqrt[]{243/3}=9$ ...
$dV/dh=(1/3).\pi.{r}^{2}=(1/3).\pi.81=27.\pi$ ...
voltando a 1º eq.
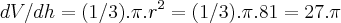$40.\pi=27.\pi.h'(t)\Rightarrow h'(t) \simeq 1.48$ ...bom é isso,obrigado