 por uchihacx » Qui Dez 17, 2015 00:23
por uchihacx » Qui Dez 17, 2015 00:23
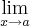
(x^k - a^k ) = 0
-
uchihacx
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Dez 17, 2015 00:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: cursando
 por e8group » Sex Dez 18, 2015 22:46
por e8group » Sex Dez 18, 2015 22:46
Se ,

é fácil verificar o resultado . No caso geral , em que k é um natural qualquer
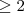
,fatore x^k - a^k ( divida o polinômio x^k - a^k por x-a ) . Feito isto , vamos poder escrever x^k - a^k como (x-a) q(x) , onde q(x) é um polinômio de grau k-1 . Em seguida ,note o seguinte , ao trabalharmos com x próximo de a , podemos majorar |x| (e.g . por 1 + |a| ) , e consequentemente teremos |q(x)| < M (p algum M > 0 ) . Dai vem :
|x^k - a^k| = |x-a| |q(x)| < M |x-a|
O segundo membro da desigualdade acima pode ficar arbitrariamente pequeno o que estabilizara o resultado .
Note que neste fórum tal questão já foi resolvida , onde há uma discussão mais detalhada .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] como essa divisão foi simplificada?
por GandalfOAzul » Sáb Set 14, 2019 01:21
- 5 Respostas
- 10402 Exibições
- Última mensagem por GandalfOAzul

Qua Set 18, 2019 12:01
Cálculo: Limites, Derivadas e Integrais
-
- Provar - Limites
por Cleyson007 » Sáb Abr 28, 2012 17:11
- 1 Respostas
- 1269 Exibições
- Última mensagem por MarceloFantini

Dom Abr 29, 2012 15:42
Cálculo: Limites, Derivadas e Integrais
-
- Limite Notável-Como provar?
por joaofonseca » Dom Out 30, 2011 20:19
- 4 Respostas
- 4058 Exibições
- Última mensagem por joaofonseca

Ter Nov 01, 2011 08:14
Cálculo: Limites, Derivadas e Integrais
-
- Funções impares- como provar
por Thayna Santos » Seg Mar 16, 2015 12:10
- 1 Respostas
- 1901 Exibições
- Última mensagem por adauto martins

Seg Mar 16, 2015 15:41
Funções
-
- [limites] provar que existe o limite
por heric » Qui Out 13, 2011 14:36
- 4 Respostas
- 3439 Exibições
- Última mensagem por LuizAquino

Seg Out 17, 2011 11:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
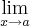 (x^k - a^k ) = 0
(x^k - a^k ) = 0

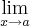 (x^k - a^k ) = 0
(x^k - a^k ) = 0
 é fácil verificar o resultado . No caso geral , em que k é um natural qualquer
é fácil verificar o resultado . No caso geral , em que k é um natural qualquer 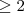 ,fatore x^k - a^k ( divida o polinômio x^k - a^k por x-a ) . Feito isto , vamos poder escrever x^k - a^k como (x-a) q(x) , onde q(x) é um polinômio de grau k-1 . Em seguida ,note o seguinte , ao trabalharmos com x próximo de a , podemos majorar |x| (e.g . por 1 + |a| ) , e consequentemente teremos |q(x)| < M (p algum M > 0 ) . Dai vem :
,fatore x^k - a^k ( divida o polinômio x^k - a^k por x-a ) . Feito isto , vamos poder escrever x^k - a^k como (x-a) q(x) , onde q(x) é um polinômio de grau k-1 . Em seguida ,note o seguinte , ao trabalharmos com x próximo de a , podemos majorar |x| (e.g . por 1 + |a| ) , e consequentemente teremos |q(x)| < M (p algum M > 0 ) . Dai vem : 