 por andrerodrigues98 » Sáb Mai 02, 2015 16:35
por andrerodrigues98 » Sáb Mai 02, 2015 16:35
Por quê a derivada de
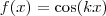
, com
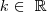
, e sendo uma constante, resulta em

?
-
andrerodrigues98
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qui Nov 13, 2014 16:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Cleyson007 » Sáb Mai 02, 2015 19:58
por Cleyson007 » Sáb Mai 02, 2015 19:58
Olá, boa noite!
Seja a função f(x) = cos(kx)
Na verdade, temos uma composição de funções.
Estou usando a Regra Cadeia, veja:
Vamos chamar u = kx (Parte interna "dentro do parêntese").
Derivando "u" em relação a "x", temos: du/dx = k
Seja v = cos (u)
dv/du = -sen (u)
O resultado final é dado pela multiplicação de (du/dx)(dv/du) = k (-sen (u)), mas como u = kx temos: (du/dx)(dv/du) =
k (-sen (kx))Qualquer dúvida estou a disposição.
Caso queira conhecer melhor o meu trabalho:
e-mail:
descomplicamat@hotmail.comWhatsApp: (38) 9889-5755
Abraço
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por andrerodrigues98 » Dom Mai 03, 2015 13:35
por andrerodrigues98 » Dom Mai 03, 2015 13:35
Obrigado. Agora entendi!
-
andrerodrigues98
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qui Nov 13, 2014 16:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10887 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13193 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14798 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5115 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
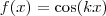 , com
, com 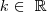 , e sendo uma constante, resulta em
, e sendo uma constante, resulta em  ?
?
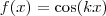 , com
, com 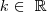 , e sendo uma constante, resulta em
, e sendo uma constante, resulta em  ?
?


