Calcule a area da região limitada pelas curvas
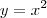 e
e  .
. Eu tentei fazer colocando o
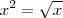 . Sei que é simples, mas meio que esqueci :( . O que faz a partir dai? e no caso eu não tenho a resposta, ai não sei como fazer e nem se estaria chegando no resultado certo. Agradeço quem puder deixar o passo a passo.
. Sei que é simples, mas meio que esqueci :( . O que faz a partir dai? e no caso eu não tenho a resposta, ai não sei como fazer e nem se estaria chegando no resultado certo. Agradeço quem puder deixar o passo a passo.

 ,o ponto onde as curvas se igulam ou seja
,o ponto onde as curvas se igulam ou seja ![{x}^{2}=\sqrt[]{x} {x}^{2}=\sqrt[]{x}](/latexrender/pictures/2754f1126d721295c7db5f4a47ae5323.png) ...logo teremos
...logo teremos 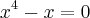 ,cujas raizes serao x=0,x=1(raiz de multiplicidade 3)...no intervalo [0,1]
,cujas raizes serao x=0,x=1(raiz de multiplicidade 3)...no intervalo [0,1]![\sqrt[]{x}\succ {x}^{2}\Rightarrow A=\int_{0}^{1}(\sqrt[]{x}-{x}^{2})dx \sqrt[]{x}\succ {x}^{2}\Rightarrow A=\int_{0}^{1}(\sqrt[]{x}-{x}^{2})dx](/latexrender/pictures/a7616fe17a20b74a09d11516a9486591.png) ...
...![A=\int_{0}^{1}({x}^{1/2})dx-\int_{0}^{1}({x}^{2})dx=(2/3){x}^{3/2}-(1/3){x}^{3}[0,1]=(2/3)-(1/3)=1/3 A=\int_{0}^{1}({x}^{1/2})dx-\int_{0}^{1}({x}^{2})dx=(2/3){x}^{3/2}-(1/3){x}^{3}[0,1]=(2/3)-(1/3)=1/3](/latexrender/pictures/0502650a161801cf03ebe167110caca1.png)

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)