por joandro » Dom Abr 13, 2014 11:30
por alienante » Ter Abr 29, 2014 17:27
![f(x)=x^4-4x^3+10\rightarrow \frac{d}{dx}[f(x)]=4x^3-12x^2\rightarrow \frac{d^2}{dx^2}[f(x)]=12x^2-24x](/latexrender/pictures/4149e995d1254a1fa3abc647532048f4.png "f(x)=x^4-4x^3+10\rightarrow \frac{d}{dx}[f(x)]=4x^3-12x^2\rightarrow \frac{d^2}{dx^2}[f(x)]=12x^2-24x")
. Achando os pontos críticos com a derivada primeira temos que:![\frac{d}{dx}[f(x)]=4x^3-12x^2=0\rightarrow 4x^2(x-3)=0](/latexrender/pictures/27c254e4f53e82f8be3d3565fba04fb3.png "\frac{d}{dx}[f(x)]=4x^3-12x^2=0\rightarrow 4x^2(x-3)=0")
oque significa qu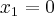e 
e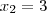 
. Se pegarmos qualquer ponto no intervalo 
perceberemos que ![\frac{d}{dx}[f(x)]<0](/latexrender/pictures/4349fc45a47b18ed7290c579ec15eca3.png "\frac{d}{dx}[f(x)]<0")
, portanto nesse intervalo a função é decrescente, no intervalo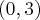 
veremos que , logo nesse intervalo também será decrescente, e no intervalo 
percebemos que ![\frac{d}{dx}[f(x)]>0](/latexrender/pictures/1ffc35c57f6baec78af4c2ec8a96ec33.png "\frac{d}{dx}[f(x)]>0")
, logo a função será crescente nesse intervalo.Quanto a concavidade termos de achar os pontos de inflexão com a derivada segunda:![\frac{d^2}{dx^2}[f(x)]=12x^2-24x=0\rightarrow 12x(x-2)=0](/latexrender/pictures/69a18c99b8894a65fb8446bef8b28448.png "\frac{d^2}{dx^2}[f(x)]=12x^2-24x=0\rightarrow 12x(x-2)=0")
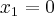logo e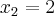 
. Se analasarmos o intervalo veremos que ![\frac{d^2}{dx^2}[f(x)]>0](/latexrender/pictures/1698d350d78fe5935bb758096de9f821.png "\frac{d^2}{dx^2}[f(x)]>0")
logo a função será concava para cima nesse intervalo.No intervalo
veremos que ![\frac{d^2}{dx^2}[f(x)]<0](/latexrender/pictures/8081be120e041f3bd75ae35767df8ba0.png "\frac{d^2}{dx^2}[f(x)]<0")
logo a função será concava para baixo nesse intervalo, e no intervalo
veremos que logo veremos que a função será concava para cima nesse intervalo.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes