 por Sobreira » Dom Dez 08, 2013 14:27
por Sobreira » Dom Dez 08, 2013 14:27
Amigos,
Tenho a seguinte dúvida:
Há uma afirmação que no capacitor não pode haver variação brusca de tensão em seus terminais. Lendo no livro o autor justifica que isto não é possível pois haverá a necessidade de uma corrente infinita. Mas aí que não entendi:
Pelo meu entender isto parte do problema que a derivada estará no ponto de descontinuidade da função, ou seja, indefinido e nisto a corrente terá que ir a infinito para compensar.
Mas e quando não há variação de tensão ??? Quando o gráfico v/t é uma reta?? a derivada também será 0 e portanto precisaríamos de uma corrente infinita, ou seja, para uma tensão constante a corrente no capacitor seria infinito e não zero.

- Anexos
-
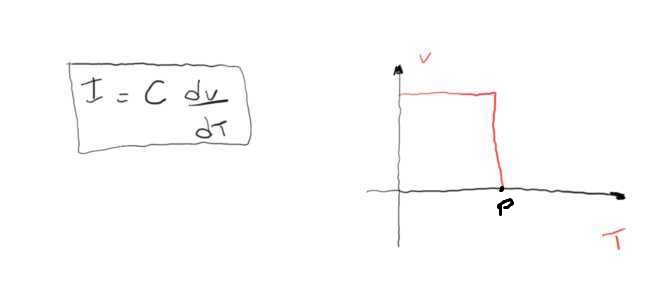
- capacitor.jpg (11.5 KiB) Exibido 7311 vezes
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por young_jedi » Ter Dez 10, 2013 17:52
por young_jedi » Ter Dez 10, 2013 17:52
no primeiro caso, em que ha descontinuidade da função nos temos que a derivada tende para infinito

no caso da reta a derivada é igual a zero portanto a corrente é igual a zero.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Armadura de um capacitor
por Guga1981 » Ter Abr 16, 2019 04:53
- 0 Respostas
- 11962 Exibições
- Última mensagem por Guga1981

Ter Abr 16, 2019 04:53
Eletricidade I
-
- [Derivada] Definição de derivada num ponto
por fff » Seg Fev 24, 2014 17:12
- 2 Respostas
- 2797 Exibições
- Última mensagem por e8group

Dom Jul 20, 2014 16:14
Cálculo: Limites, Derivadas e Integrais
-
- Derivada em um ponto
por rodrigo lara » Sex Dez 27, 2013 20:31
- 3 Respostas
- 1866 Exibições
- Última mensagem por e8group

Ter Jan 07, 2014 22:21
Cálculo: Limites, Derivadas e Integrais
-
- Derivada em um ponto
por Fernandobertolaccini » Qui Jul 10, 2014 13:15
- 3 Respostas
- 1638 Exibições
- Última mensagem por young_jedi

Qui Jul 10, 2014 21:54
Cálculo: Limites, Derivadas e Integrais
-
- [Existência de Derivada em um Ponto]
por raimundoocjr » Qui Mai 30, 2013 18:19
- 3 Respostas
- 1622 Exibições
- Última mensagem por Jhonata

Qui Mai 30, 2013 19:21
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 .
.



