Seja a, b, c, e d constantes tais que

encontre o valor da soma a+b+c+d
resposta = 24



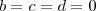 , o limite dado se resume a
, o limite dado se resume a 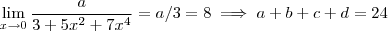 . Agora suponha
. Agora suponha  .Neste caso ,
.Neste caso ,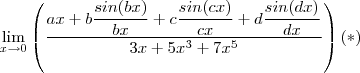 .
. 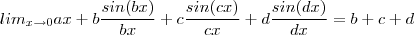 existe e é finito e
existe e é finito e 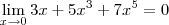 , concluímos que o limite
, concluímos que o limite  não é finito, contradição ! Portanto ,
não é finito, contradição ! Portanto ,  e
e 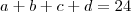 .
.


 existir e ser finito , a saber o limite desta expressão quando
existir e ser finito , a saber o limite desta expressão quando  tende a zero é o número real
tende a zero é o número real  que pode ser nulo mesmo considerando
que pode ser nulo mesmo considerando 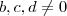 , e caso
, e caso 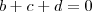 não podemos dizer nada sobre o limite
não podemos dizer nada sobre o limite  tendo em conta que o mesmo apresentar forma indeterminada "0/0" , portanto devemos também supor
tendo em conta que o mesmo apresentar forma indeterminada "0/0" , portanto devemos também supor 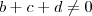 bem como
bem como 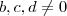 e chegar em absurdo ,conforme já vimos.
e chegar em absurdo ,conforme já vimos. se ocorrem as duas situações :
se ocorrem as duas situações :  existe e é um número finito não nulo , digamos
existe e é um número finito não nulo , digamos  , e
, e 

 não é nulo e aplicarmos a regra de L´Hospital 2x sobra
não é nulo e aplicarmos a regra de L´Hospital 2x sobra  como constante no numerador e
como constante no numerador e 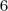 no denominador, e para o limite resultar em
no denominador, e para o limite resultar em  , a unica hipótese que se encaixa no problema é a de que
, a unica hipótese que se encaixa no problema é a de que  e
e  são nulos. Se as variáveis nos senos estivessem elevadas ao quadrado, daí sim poderíamos considerar
são nulos. Se as variáveis nos senos estivessem elevadas ao quadrado, daí sim poderíamos considerar  e
e  não nulos.
não nulos.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

