Também estou com a mesma dúvida ,resolvi este exercício da seguinte forma :
Supondo que a curva

(obtida pelo deslocamento do vértice P) tenha uma parametrização dada por
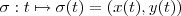
. Como o ponto

pertence simultaneamente a elipse e a reta
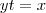
dada .Então , fazendo as contas conforme você fez , vamos obter
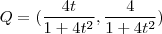
. Ora , os pontos
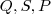
estão variando em conjunto de modo a preservar a ortogonalidade entre
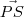
e

(estou utilizando este argumento para utilizar o próximo resultado afirmando que as ordenadas entre P,Q são iguais ) à medida que

varia . Logo ,
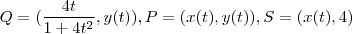
com
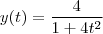
.
E facilmente obtemos
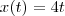
pelo que o ponto

pertence as duas retas dadas .
Vou conversar com meu prof. de cal. sobre este exercício .Obtendo resultados postarei .
![[tex]4x^2+(y-2)^2=4\Rightarrow x^2+\frac{(y-2)^2}{4}=1\Rightarrow y^2t^2+\frac{y^2-4y+4}{4}=1\Rightarrow 4y^2t^2 + y^2- 4y +4 = 4 \Rightarrow 4y^2t^2 + y^2- 4y=0\Rightarrow y =\frac{x}{t} \Rightarrow \frac{x^2}{t^2} + 4x^2 - 4\frac{x}{t}=0 \Rightarrow x\left(\frac{x}{t^2} + 4x - \frac{4}{t} \right)=0 \Rightarrow \frac{x}{t^2} + 4x - \frac{4}{t}=0 \Rightarrow x\left(4+\frac{1}{t^2} \right)=\frac{4}{t} \Rightarrow x= \frac{4}{t}\ \times \frac{1}{\left 4t^2+1 \right} \Rightarrow y =\frac{4}{1+4t^2} [tex]4x^2+(y-2)^2=4\Rightarrow x^2+\frac{(y-2)^2}{4}=1\Rightarrow y^2t^2+\frac{y^2-4y+4}{4}=1\Rightarrow 4y^2t^2 + y^2- 4y +4 = 4 \Rightarrow 4y^2t^2 + y^2- 4y=0\Rightarrow y =\frac{x}{t} \Rightarrow \frac{x^2}{t^2} + 4x^2 - 4\frac{x}{t}=0 \Rightarrow x\left(\frac{x}{t^2} + 4x - \frac{4}{t} \right)=0 \Rightarrow \frac{x}{t^2} + 4x - \frac{4}{t}=0 \Rightarrow x\left(4+\frac{1}{t^2} \right)=\frac{4}{t} \Rightarrow x= \frac{4}{t}\ \times \frac{1}{\left 4t^2+1 \right} \Rightarrow y =\frac{4}{1+4t^2}](/latexrender/pictures/0adb4051dcf9476c38bc2f185a07c3db.png)
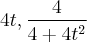


 (obtida pelo deslocamento do vértice P) tenha uma parametrização dada por
(obtida pelo deslocamento do vértice P) tenha uma parametrização dada por 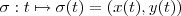 . Como o ponto
. Como o ponto  pertence simultaneamente a elipse e a reta
pertence simultaneamente a elipse e a reta 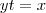 dada .Então , fazendo as contas conforme você fez , vamos obter
dada .Então , fazendo as contas conforme você fez , vamos obter 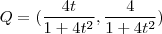 . Ora , os pontos
. Ora , os pontos 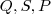 estão variando em conjunto de modo a preservar a ortogonalidade entre
estão variando em conjunto de modo a preservar a ortogonalidade entre 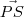 e
e  (estou utilizando este argumento para utilizar o próximo resultado afirmando que as ordenadas entre P,Q são iguais ) à medida que
(estou utilizando este argumento para utilizar o próximo resultado afirmando que as ordenadas entre P,Q são iguais ) à medida que  varia . Logo ,
varia . Logo , 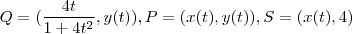 com
com 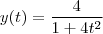 .
. 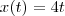 pelo que o ponto
pelo que o ponto  pertence as duas retas dadas .
pertence as duas retas dadas .