marcosmuscul escreveu:seja
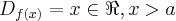
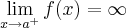
existe ou não assintota vertical em x = a?
Sim, existe.
Por
definição, dizemos que a reta x = a é uma assíntota vertical do gráfico da função f se qualquer um dos dois casos abaixo acontecer:
(i)

(ii)
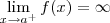
Em outras palavras, note que x = a será uma assíntota vertical quando qualquer um dos limites laterais for infinito.
Observação: aqui o símbolo

pode ser

ou

dependendo do caso.
marcosmuscul escreveu:fiquei na duvida pois no livro da dizendo que pra existir limite infinito, ou seja , assintota vertical, o limite precisa ir ao infinito positivo ou negativo tanto pela direita quanto pela esquerda de a.
Você está confundindo dois conceitos diferentes:
existir o limite (e ele ser igual a infinito);
ter uma assíntota vertical.
Para
ter uma assíntota vertical, basta respeitar a definição apresentada anteriormente.
Já para
existir o limite, devemos ter que seus laterais são iguais.
Em outras palavras, temos que

existe e é igual a L, quando ocorrer
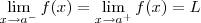
. Aqui não importa se L representa um número real fixo ou o conceito de infinito.
Por exemplo, para que

exista e seja igual a

, devemos ter

.
marcosmuscul escreveu:outra duvida é:
Em relação a uma função definida para x diferente de a.
se pela esquerda o limite é infinito negativo e pela esquerda é infinito positivo. Posso dizer que existe assíntota vertical?
Eu presumo que você quis dizer "(...) e pela direita é infinito positivo (...)".
Neste caso, observando a definição de reta assíntota, então a resposta é sim.
Mas note que neste caso, analisando a existência do limite, temos que o limite quando x tende para a não existe.
Por exemplo, na função

temos que:
(i) x = 1 é uma assíntota vertical;
(ii) Não existe

.
ObservaçãoEu gostaria de sugerir que você assista as videoaulas "03. Cálculo I - Limites Laterais" e "05. Cálculo I - Limites Infinitos". Elas estão disponíveis na página do meu projeto:
http://www.lcmaquino.org/Eu espero que essas videoaulas possam lhe ajudar a entender melhor os conceitos.
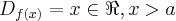
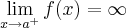



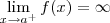
 pode ser
pode ser  ou
ou  dependendo do caso.
dependendo do caso. existe e é igual a L, quando ocorrer
existe e é igual a L, quando ocorrer 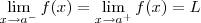 . Aqui não importa se L representa um número real fixo ou o conceito de infinito.
. Aqui não importa se L representa um número real fixo ou o conceito de infinito. .
. temos que:
temos que: .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
