 = 2u
= 2u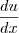 .
.Solução
y = u
 u
u 
 =
= 
Assim,
 = 2u
= 2u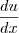 ."
."Bom, sei que
 significa f'(x) ou derivada de y em relação a x. E sei que
significa f'(x) ou derivada de y em relação a x. E sei que 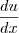 significa u'(x) ou derivada de y em relação a x. Mas não sei como interpretar 2u
significa u'(x) ou derivada de y em relação a x. Mas não sei como interpretar 2u 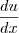 ... não compreendo a igualdade que o exemplo quer mostrar. Porque, para mim, 2u
... não compreendo a igualdade que o exemplo quer mostrar. Porque, para mim, 2u 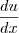 = 2u
= 2u  u'(x) ou u = 2u². Essa notação ajuda para resolver vários exercícios mas eu não a entendo completamente... Grato a quem puder ajudar !
u'(x) ou u = 2u². Essa notação ajuda para resolver vários exercícios mas eu não a entendo completamente... Grato a quem puder ajudar !

 é o mesmo que
é o mesmo que  notação esta que vc está mais familiarizado .
notação esta que vc está mais familiarizado .  .Assim ,
.Assim ,  . Pela regra da cadeia ,
. Pela regra da cadeia , 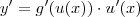 que é o mesmo que
que é o mesmo que  .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)